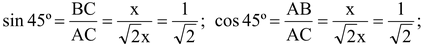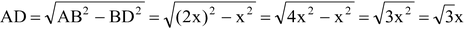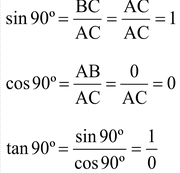Trigonometric Ratios Of Some Specific Angles
Trigonometry of Class 10
Trigonometric Ratios Of Some Specific Angles
TRIGONOMETRIC RATIOS OF 45º:
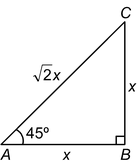
Let ΔABC be a right-angled triangle in which ∠B = 90º and ∠A = 45º.
Then, ∠C = 45º [Angle sum property]
∠A = ∠C ⇒ AB = BC. [Side opposite to equal angles]
|
Let AB = BC = x units. Then,
AC =
∴ base = AB = x units; perpendicular = BC = x units and hypotenuse = AC = √2x units.
∴
|
|
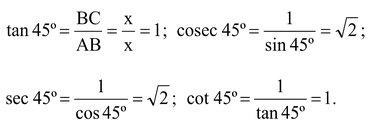
TRIGONOMETRIC RATIOS OF 60º AND 30º:
|
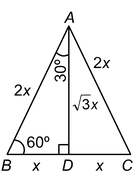
Consider an equilateral ΔABC with each side equal to 2x. Then, each angle of ΔABC is 60º. From A, draw AD ⊥ BC. Then, clearly, BD = DC = x. Also, ∠ADB = 90º. ∴ ∠BAD = 30º. [Angle sum property] From right-angled ΔADB, we have:
|
|
T-RATIOS OF 60º:
In right-angled ΔADB, we have
base = BD = x; perpendicular = AD = √3x and hypotenuse = AB = 2x
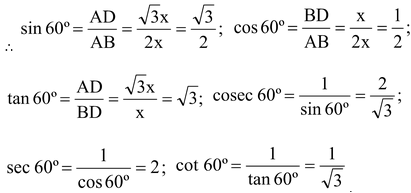
T-RATIOS OF 30º:
In right-angled ΔADB, we have
base = AD = √3x, perpendicular = BD = x and hypotenuse = AB = 2x.
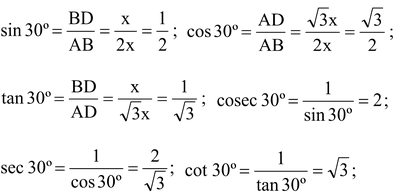
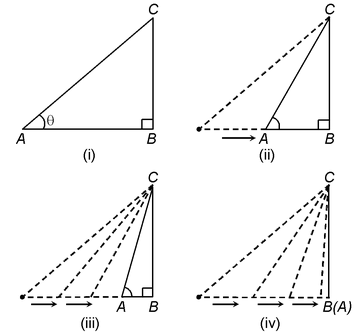
TRIGONOMETRIC RATIOS OF 0º:
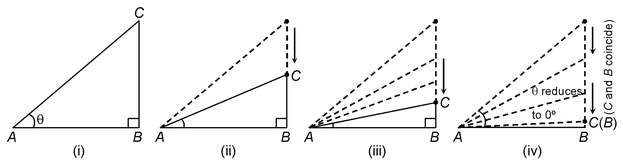
In the figure (i), ΔABC is right angled at B and ∠BAC = θ.
In figure (ii), ∠BAC is reduced and it is less than θ. Here, we observe that the point C moves closer to the point B.
In figure (iii), ∠BAC is very small and the point C is also very close to the point B.
In figure (iv), ∠BAC just reduces to 0º and the point C coincides with the point B, i.e.,
BC = 0 and AB = AC. Then by definition, the values of the trigonometric ratios of 0º are as under:
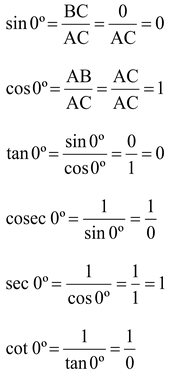
Hence, we have
sin 0º = 0, cos 0º = 1, tan 0º = 0, sec 0º = 1.
The values of cosec 0º and cot 0º are not defined as real numbers.
TRIGONOMETRIC RATIOS OF 90º:
|
We observe from the figures (i, ii, iii, iv) that as the point A moves closer to the point B, the angle ∠BAC becomes larger and larger and ultimately when A coincides with B, the angle ∠BAC becomes equal to 90º. Thus, when ∠BAC = 90º, we have AB = 0, BC = AC because AC and BC coincide. Now, we get
|
|
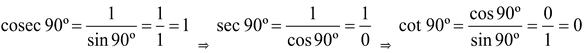 .
.
Hence, we have the values of the trigonometric ratios of 90º as under:
sin 90º = 1, cos 90º = 0, cosec 90º = 1, cot 90º = 0.
The values of sec 90º and tan 90º are not defined as real numbers.
|
|
|

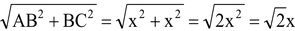 units.
units.