RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.5:
The Physics Wallah academic team has provided a comprehensive answer for Chapter 3: Squares and Square Roots in the RS Aggarwal class 8 textbook. The RS Aggarwal class 8 solution for Chapter 3 Squares and Square Roots Exercise-3E is uploaded for reference only; do not copy the solutions.
Before going through the solution of chapter-3 Squares and Square Roots Exercise-3E, one must have a clear understanding of Chapter 3 Squares and Square Roots. Read the theory of Chapter 3 Squares and Square Roots and then try to solve all numerical of exercise-3E. For class 8 maths students, the NCERT textbook is a highly recommended resource for solving numerical problems and referencing NCERT solutions.
RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.5 Squares and Square Roots Overview
RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.5 "Squares and Square Roots." Exercise 3.5 specifically delves into solving problems related to these concepts. This exercise is designed to enhance students' understanding and computational skills in finding squares and square roots of numbers.
The exercise begins with straightforward problems requiring students to find the squares of given numbers, emphasizing the fundamental concept of squaring. It then progresses to more complex problems involving square roots, where students practice methods such as prime factorization and the long division method to determine the square roots of both perfect and non-perfect squares.
Additionally, the exercise includes problems that challenge students to apply their knowledge in practical scenarios, such as finding the side length of a square when given the area or solving word problems that require the use of square roots.
RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.5 PDF
RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.5 focuses on "Squares and Square Roots," aiming to build a strong foundation in these fundamental concepts. This exercise covers a variety of problems, including calculating squares and square roots of numbers, applying prime factorization, and using the long division method. It also incorporates practical applications such as finding the side length of a square given its area and solving word problems.
Below we have provided RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.5 in detail. This chapter will help you to clear all your doubts regarding the chapter. Students are advised to prepare from these RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.5 before the examinations to perform better.
RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.5 PDF
RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.5 (Ex 3E)
Below we have provided RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.5 Squares and Square Roots –
Evaluate:
Question (1)
√576
Question (2) √1444
Question (3) √4489
Question (4) √6241
Question (5) √7056
Question (6) √9025
Question (7) √11449
Question (8) √14161
Question (9) √10404
Question (10) √17956
Question (11) √19600
Question (12) √92416
Question (13) Find the least number which must be subtracted from 2509 to make it a perfect square.
Let us try to find the square root of 2509.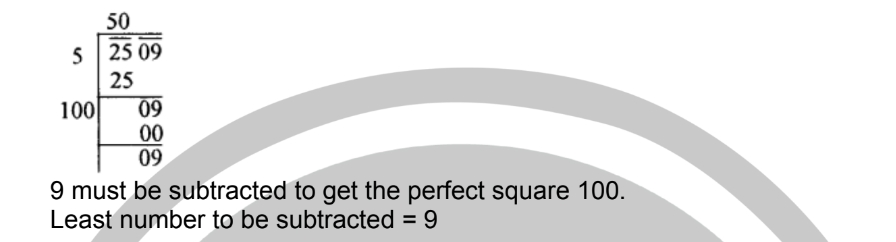
Question (14) Find the least number which must be subtracted from 7581 to obtain a perfect square. Find this perfect square ant its square root.
Let us try to find the square root of 7581.
Question (15) Find the least number which must be added to 6203 to obtain a perfect square. Find this perfect square and its square root.
Question (16) Find the least number which must be added to 8400 to obtain a perfect square. Find this perfect square and its square root.
Question (17) Find the least number of four digits which is a perfect square. Also find the square root of the number so obtained.
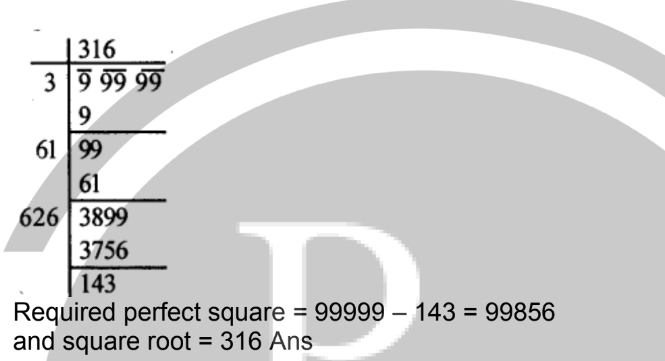
Question (18) Find the greatest number of five digits which is perfect square. Also find the square root of the number so obtained.
Question (19) The area of a square field is 60025 m
2
. A man cycles along its boundary at 18 km/h. In how much time will he return to the starting point?
Benefits of RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.5
The RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.5 on Squares and Square Roots offers several benefits to students:
Comprehensive Understanding
: The solutions provide detailed explanations for each problem, helping students understand the underlying concepts of squares and square roots thoroughly.
Step-by-Step Guidance
: Each solution is broken down into manageable steps, making it easier for students to follow and learn the correct procedures for solving similar problems.
Enhanced Problem-Solving Skills
: By working through a variety of problems, students can develop and improve their problem-solving skills, which are crucial for higher-level mathematics.
Clarity in Concepts
: The solutions clarify complex concepts by providing clear and concise explanations, ensuring that students can grasp the material effectively.
Confidence Building
: Regular practice with these solutions helps students build confidence in their abilities to tackle square and square root problems independently.
Exam Preparation
: The solutions are aligned with the curriculum and exam patterns, providing students with relevant practice that prepares them for school exams and standardized tests.
