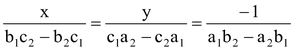Linear Equations In Two Variables
Share
Linear Equations In Two Variables
Pair Of Linear Equations In Two Variables of Class 10
1. The equation of the form ax = b or ax + b = 0, where a and b are two real numbers such that x ≠ 0 and x is a variable is called a inear equation in one variable.
2. The general form of a linear equation in two variables is ax + by +c = 0 or ax + by = c where a, b, c are real numbers and a ≠ 0, b ≠ 0 and x, y are variables.
3. The graph of a linear equation in two variables is a straight line.
4. The graph of a linear equation in one variable is a straight line parallel to x-axis for ay = b and parallel to y-axis for ax = b, where a ≠ 0.
5. A pair of linear equations in two variables is said to form a system of simultaneous linear equations.
6. The value of the variable x and y satisfying each one of the equations in a given system of linear equations in x and y simultaneously is called a solution of the system.
Standard form of linear equation:
(Standard form refers to all positive coefficient)
a 1 x + b 1 y + c 1 = 0 ....(i)
a 2 x + b 2 y + c 2 = 0 ....(ii)
For solving such equations we have three methods.
(i) Elimination by substitution
(ii) Elimination by equating the coefficients
(iii) Elimination by cross multiplication.
ELIMINATION BY SUBSTITUTION:
(Find the value of any one variable in terms of other and then use it to find other variable from the second equation):
question 1. Solve x + 4y = 14 .....(i)
7x - 3y = 5 ....(ii)
Solution: From equation (i) x = 14 - 4y ....(iii)
Substitute the value of x in equation (ii)
⇒ 7 (14 - 4y) - 3y = 5
⇒ 98 - 28y - 3y = 5
⇒ 98 - 31y = 5
⇒ 93 = 31y
⇒ y = 93/31
⇒ y = 3
Now substitute value of y in equation (iii)
⇒ 7x - 3 (3) = 5
⇒ 7x - 3 (3) = 5
⇒ 7x = 14
⇒ x = 14/7 = 2
So the solution is x = 2 and y = 3
ELIMINATION BY EQUATING THE COEFFICIENTS:
(Eliminating One variable by making the coefficient equal to get the value of one variable and then put it in any equation to find other variable):
question 1. Solve 9x - 4y = 8 ...(i)
13x + 7y = 101 ...(ii)
Solution: Multiply equation (i) by 7 and equation (ii) by 4, we get
adding 63x – 28y = 56
52x + 28y = 404
115x = 460
⇒ .x = 460/115
⇒ x = 4
Substitute x = 4 in equation (i)
9 (4) –0 4y = 8 ⇒ 36 – 8 = 4y ⇒ 28 = 4y
⇒ y = 28/4 = 7
So the solution is x = 4 and y = 7.
COMPARISON METHOD:
(Find the value of one variable from both the equation and equate them to get the value of other variable):
Let any pair of linear equations in two variables is of the form
a 1 x + b 1 y + c 1 = 0 .........(i)
a 2 x + b 2 y + c 2 = 0 .....…(ii)
question 1. Solve for x and y : 2x + 3y = 8 , x - 5y = -9.
Solution: 2x + 3y = 8 …(i)
x - 5y = -9. …(ii)
From equation (i),
2x = 8 - 3y , x = 8 - 3y/2 …(iii)
From equation (ii),
x = -9 + 5y…(iv)
From equation (iii) and (iv), we have
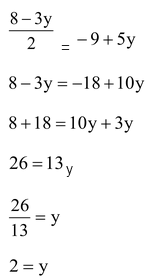
Putting value of y in equation (iv), we have
x = 8 - 3 x 2/2
x = 1
Solution x = 1, y = 2.
CROSS MULTIPLICATION METHOD:
Let the equation
a 1 x + b 1 y + c 1 = 0 …(i)
a 2 x + b 2 y + c 2 = 0 …(ii)
To obtain the values of x and y, we follow these steps:
1. Multiply Equation (i) by b 2 and (ii) by b1, we get
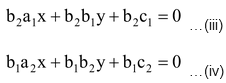
2. Subtracting Equation (iv) from (iii), we get:
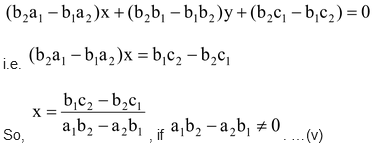
3. Substituting this value of x in (i) or (ii), we get
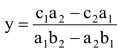. …(vi)
We can write the solution given by equations (v) and (vi) in the following form:
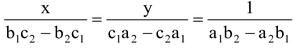…(vii)
In remembering the above result, the following diagram may be helpful:
For solving a pair of linear equations by this method, we will follow the following steps:
1. Write the given equations in the form (i) and (ii).
2. Taking the help of the diagram above, write equations as given in (viii).
3. Find x and y.
|
|
For the equations like a 1 x + b 1 y + c 1 = 0 and a 2 x + b 2 y + c 2 = 0 The solution set can be calculated by using
(Please note position of c1 and c2 with equality sign and subsequent change in the third term i.e. –1) |
question 1. Solve the following system of equations in x and y
ax + by - a + b = 0, bx - ay - a - b = 0
Solution: a 1 = a, b 1 = b, a 2 = b and b 2 = –a
∴
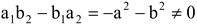
Hence, the given system of the equation has unique solution.
By cross multiplication, we have
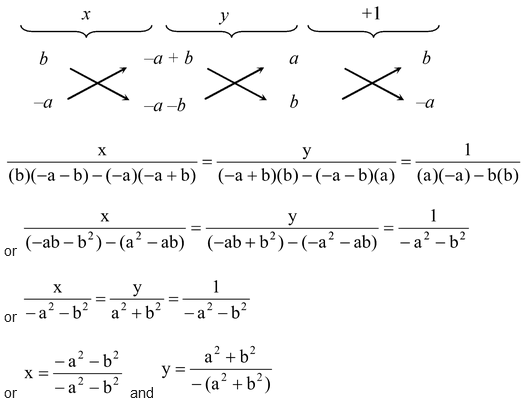
or x = 1 and y = –1
question 2. Solve for x and y.
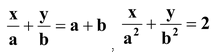
Solution: Here a1 =1/a, b1 =1/b, a2 = 1/a 2 and b2 = 1/b 2
∴
.
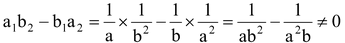Hence, the given system of equation has unique solution.
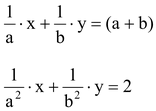
By cross multiplication, we have
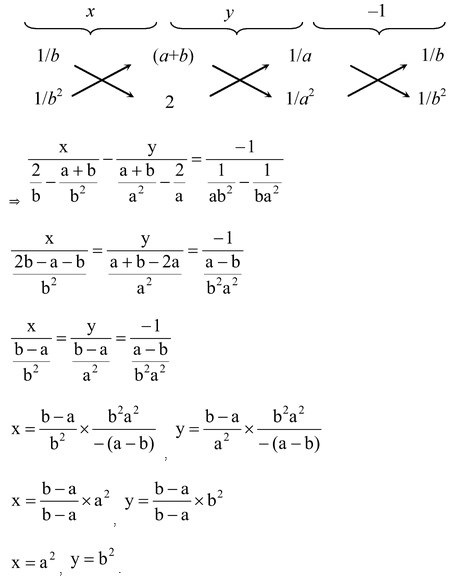
question 3. Solve the following system of equations by using cross multiplication method:
5x + 3y = 19, 16x - 7y = 11
Solution: Here a 1 = 5, b 1 = 3 and a 2 = 16, b 2 = –7
∴
.
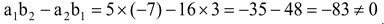Hence, the given system of equation has a unique solution. By cross multiplication, we have
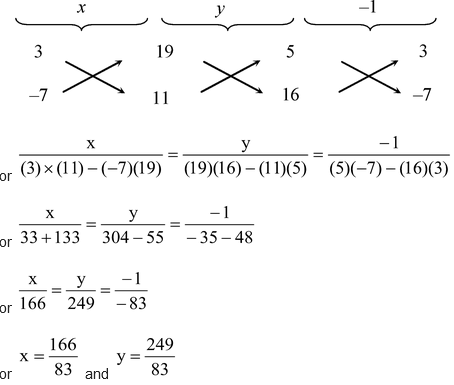
or x = 2 and y = 3
Do solve NCERT text book for class 10 maths with the help of pw NCERT solutions for class 10 maths.
