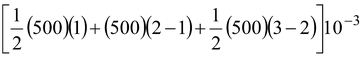Impulse
Impluse And Momentum of Class 11
In the previous chapter, we have learnt the concept of work which was an integral of force with respect to displacement. Now we are going to learn another concept, called impulse.
Impulse is defined as the integral of force with respect to time.
![]() =
=
![]() (9.1)
(9.1)
Since force is a vector and time is a scalar, the result of the integral in equation (9.1) is a vector. If the force is constant (both in magnitude and direction), it may be removed from the integral so that the integral is reduced to
I =
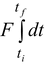 = F(tf - ti) = FΔt (9.2)
= F(tf - ti) = FΔt (9.2)
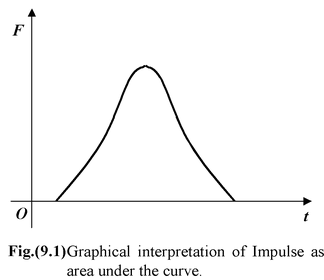
Graphically, the impulse is the area between the force curve and the F = 0 axis, as shown in figure. (9.1).
The SI unit of impulse is Ns.
Example 9.1
Find the impulse due to the force
![]() =
=
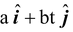 , where a = 2N and b = 4 N/s, if this force acts from ti = 0 to tf = 0.3 s.
, where a = 2N and b = 4 N/s, if this force acts from ti = 0 to tf = 0.3 s.
Solution
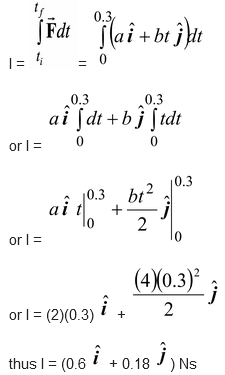
Example 9.2
|
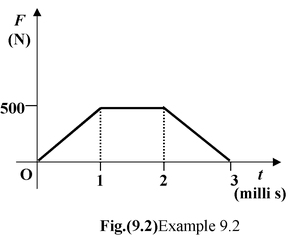
Figure shows the variation of force acting on a body with time. Calculate the impulse of this force. Solution Impulse of a force is the area under the graph. Thus
I =
or I = [250 + 500 + 250]10 -3 or I = 1 Ns |
|
If more than one force are acting on a particle, then the net impulse is given by the time integral of the net force.
![]() =
=
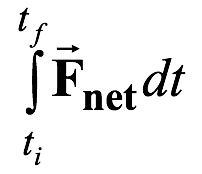 (9.3)
(9.3)