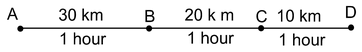DISTANCE AND DISPLACEMENT

DIFFERENCE BETWEEN DISTANCE AND DISPLACEMENT

UNIFORM MOTION:

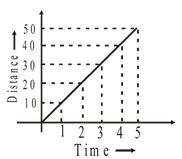
A body has a uniform motion if it travels equal distances in equal intervals of time, no matter how small these time intervals may be. For example, a car running at a constant speed of say, 10 meters per second, will cover equal distances of 10 metres every second, so its motion will be uniform. Please note that the distance-time graph for uniform motion is a straight line 

NON-UNIFORM MOTION:

Body has a non-uniform if it travels unequal distances in equal intervals of time. For example, if we drop a ball from the roof of a building, we will find that it covers unequal distances in equal intervals of time. It covers:

4.9 metres in the 1^st second

14.7 metres in the 2^nd second

24.5 metres in the 3^rd second and so on.

Thus, a freely falling ball covers smaller distance in the initial ‘1 second’ interval and larger distance in the later ‘1 second’ interval. From this discussion we conclude that the motion of a freely falling body is an example of non-uniform motion. The motions of a train starting from the railway station is also an example of non-uniform motion. This is because when the train starts from a s station, if moves a very small distance in the ‘first’ second. The train moves a little more distance in the ‘2nd’ second and so on. And when the train approaches the next station, the distance traveled by it per second decreases.

 

SPEED:

Speed of a body is defined as the distance travelled by it per unit time irrespective of direction. It is a scalar quantity.

or v = s/t

Where v is the speed, s is the distance covered and ‘t’ is the time taken. 

The S.I. unit of speed is ms^-1(metre per second). It can also be represented as centimetre per second and kilometre per hour.

The speed of a running car is shown by an instrument called “SPEEDOMETRE”. The distance travelled by the car is measured by another instrument called ODOMETRE.

Average Speed:

For an object moving with variable speed, it is the total distance traveled by the object divided by the total time taken to cover that distance.

Average speed =  total distance travelled/total time taken

Uniform Speed (or Constant Speed):

When an object covers equal distance in equal intervals of time, it is said to move with uniform speed.

Speed (A to B) = 30/1 Speed (B to C) = 30/1  Speed (C to D) =60/2

= 30 km/hr = 30 km/hr = 30 km/hr

Variable Speed (Non-Uniform Speed):

If a body covers unequal distance in equal intervals of time, its motion is said to be non-uniform.

Speed (A to B) = 30/1  Speed (B to C) = 20/1 Speed (C to D) = 10/1

= 30 km/hr = 20 km/hr =10 km/hr

Instantaneous Speed:

The speed of an object at any particular instant of time or at particular point of its path is called the instantaneous speed of the object. it is measure red by speedometer in an automobile.

VELOCITY:

Velocity of a body is defined as the displacement travelled by it per unit time. In other words velocity of a body is its speed in a given direction. It is a vector quantity. 

Velocity = Displacement/Time

or v = s/t

where v is the velocity 

s is the distance travelled 

't' is the time taken

The S.I. unit of velocity is ms^-1

Therefore, 25 km/hr is SPEED and 25 km/hr towards North is VELOCITY.

DIFFERENCE BETWEEN SPEED AND VELOCITY:

Uniform Velocity (Constant Velocity):

If a body covers equal distance in equal intervals of time in a given direction then it is said to be moving with constant velocity.

Non-Uniform Velocity:

When a body does not cover not cover equal distances in equal intervals of time, in a given direction (in this case speed is not constant), then it is known as non  uniform velocity. If speed is constant then also body can have a non-uniform velocity.

Ex. A car moving on a circular road with constant speed.

Average velocity:

It is defined as total displacement covered by particle divided by total time taken to cover that displacement.

e.g. (a) If a person is moving along a straight line AB with C as a mid-point of line AB.

Person moves from A to C with velocity v1 and C to B with velocity v2  So, average velocity of a person for whole motion  = AC + CB/t_AC + t_CB

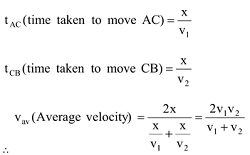
(b) If a person is moving along a straight line AB (Now C is not a mid-point of AB) person takes same time for traveling AC as well as CB while traveling AC with velocity v1 and CB with velocity v2. 

So,

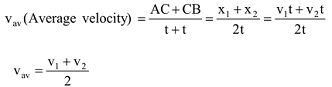
(c) If a body is having uniform acceleration or in other words if the velocity of a body is changing at a uniform rate then the average velocity is given by the ‘arithmetic mean’ of the initial velocity and final velocity for a given period of time.

i.e.

or v = u + v/2

where, v  is the average velocity

u is the initial velocity

v  is the final velocity

Instantaneous Velocity:

The velocity of an object at any given instant of time at particular point of its path is called its instantaneous velocity.

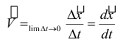
Example: When is the average speed of an object equal to the magnitude of its average velocity ? Give reason also.

Sol. As average speed = total pathlength/time interval  also, average velocity = Displacement/time interval. When an object moves along a straight line and in the same direction its total path length is equal to the magnitude of its displacement. Hence average speed is equal to the magnitude of its average velocity.

FEATURE OF UNIFORM MOTION:

• The velocity in uniform motion does not depend on the choice of origin.
• The velocity in uniform motion does not depend on the choice of the time interval (t2 – t1).
• For uniform motion along a straight line in the same direction, the magnitude of the displacement is equal to the actual distance covered by the object.
• The velocity is positive if the object is moving towards the right of the origin and negative if the object is moving towards the left of the origin.
• For an object is uniform motion no force is required to maintain its motion.
• In uniform motion, the instantaneous velocity is equal to the average velocity at all time because velocity remains constant at each instant, at each point of the path.

Question: A car is moving along x-axis. As shown in figure it moves from O to P in 18 s and returns from P to Q in 6 second. What is the average velocity and average speed of the car in going from (i) O to P and (ii) from O to P and back to Q.

Solution:  (i) Average velocity =

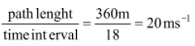
Average speed = 

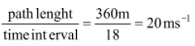
(ii) From O to P and back to Q

 

Question. A car covers the 1st half of the distance between two places at a speed of 40 km h-1 and the 2nd half at 60 km h-1. What is the average speed of the car?

Solution:  Suppose the total distance covered is 2S.

Then time taken to cover first distance with speed 40 km/h,

t₁ = s/40h

Time taken to cover second S distance with speed 60 km/h,

t₂ = s/60h

⇒ V_av = 48km/h

Question. A non-stop bus goes from one station to another station with a speed of 54 km/h, the same bus returns from the second station to the first station with a speed of 36 km/h. Find the average speed of the bus for the entire journey.

Solution: Suppose the distance between the stations is S. Time taken in reaching from one station to another station.

t₁ = S/54h

Time taken in returning back,

t₂ = S/36h

Total t = t1 + t2

ACCELERATION:

The rate of change of velocity with time is known as acceleration. In other words, the acceleration is defined as the change in velocity per unit time.

i.e.   Acceleration = change in velocity /time

or Acceleration = Final velocity - Initial velocity/time

or a = v-u/t

Where a = Acceleration of the body

v = Final velocity of the body

u= Initial velocity of the body

t = Time taken for this change in velocity

• A body is said to be accelerating if its velocity is changing
• S.I. unit of acceleration is ms^-2 (metre per second square).
•  Acceleration is a vector quantity.
•  When a body is moving with uniform velocity, its acceleration is zero (or no acceleration).

This is because there is no change in velocity as Initial velocity = Final velocity.

A body moving with non-uniform velocity is said to be in accelerated motion.

TYPES OF ACCELERATION:

• Positive acceleration : If the velocity of an object increases in the same direction, the object has a positive acceleration.
• Negative acceleration (retardation): If the velocity of a body decreases in the same direction, the body has negative acceleration or it is said to be retarding.

e.g. A train slows down.

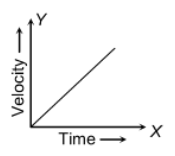
Uniform Acceleration (Uniformly Accelerated Motion):

If a body travels in a straight line and its velocity increases in equal amounts in equal intervals of time. Its motion is known as uniformly accelerated motion.

e.g. 1 Motion of a freely falling body is an example of uniformly accelerated motion (or motion of a body under the gravitational pull of the earth).

e.g. 2 Motion of a bicycle going down the slope of a road when the rider is not pedaling and wind resistance is negligible.

 

Non-uniform acceleration:

A body is said to have non-uniform acceleration if its velocity increases or decreases by unequal amount in equal intervals of time.

OR

When the velocity of a body changes at unequal rate or non-uniform rate.

e.g. most of the motion in daily life are having non uniform acceleration.

The velocity-time graph for a body having non uniform acceleration is curved line.

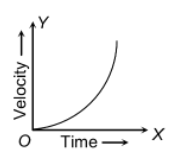
Question:  A car attains a speed of 10 ms−1 in 10 s, starting from rest. Calculate the acceleration of the car.

Solution: Given, 

Initial velocity, u=0

Final velocity, v = 10 ms−1

Time t = 10 s

We know that, acceleration, a = v-u/t

∴ a = 10-0/10 = 1 ms−2

∴ Acceleration of the car = 1 ms−2

Question. The velocity of an object is decreasing with passage of time. What conclusion do you draw about acceleration of the object?

Solution: The acceleration is negative (i.e. retardation).

Question. A car starts from rest and attains a velocity of 10 ms−1 in 40 s. The driver applies brakes and slows down the car to 5 ms−1 in 10 s. Find the acceleration of the car in both the cases.

Solution:  First case:

Initial velocity, u = 0

Final velocity, v = 10 ms−1

Time, t = 40  s

Using a = v-u/t we get

 a = (10-0)/40s ms−1

  = 0.25 ms−2

Second case:

Initial velocity, u = 10 ms−1

  Final velocity, v = 5 ms−1

Time, t = 10 s

Using a = v-u/twe get

 a = (5-10)/10s ms^-1

  =-5/10 ms−2

  = − 0.5 ms−2

In first case, car is accelerated and in the second case, the car is retarded.