MATHEMATICAL DERIVATION OF EQUATIONS OF MOTION
Motion of Class 9
When the body is moving along a straight line with uniform acceleration, a relation can be established between velocity of the body, acceleration of the body and the distance travelled by the body in a specific time by a set of equations. These equations are called equations of motion.
The Three equations are:
- First Equation of motion : v = u + at
- Second Equation of motion : s = ut + 1/2at 2
- Third Equation of motion : v 2 - u 2 = 2as
Where u = initial velocity of the body
v = final velocity of the body
a = uniform acceleration of the body
t = time taken
s = distance travelled
FIRST EQUATION OF MOTION
v = u + at
Consider a body having initial velocity ‘u’. Suppose it is subjected to a uniform acceleration ‘a’ so that after time ‘t’ its final velocity becomes ‘v’. Now we now,
Acceleration = change in velocity/time
a= v-u/t
or v = u + at or v = at + u …..(i)
This equation is known as the first equation of motion.
SECOND EQUATION OF MOTION
s = ut + 1/2at 2
Suppose a body has an initial velocity ‘u’ and uniform acceleration ‘a’ for time ‘t’ so that its final velocity becomes ‘v’. The distance traveled by moving body in time ‘t’ is ‘S’ then the average velocity = (v + u)/2. Distance traveled = Average velocity × time
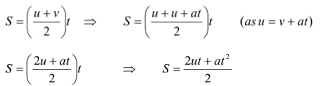
S = ut + 1/2at 2
This is the second equation of motion.
THIRD EQUATION OF MOTION
v 2 - u 2 = 2as
From the second equation of motion we have,
s = ut + 1/2at 2 …(i)
From first equation of motion, we have
v = u + at
⇒ at = v - u
⇒ t = v - u/a
Putting this value of ‘t’ in equation …(i)
We have
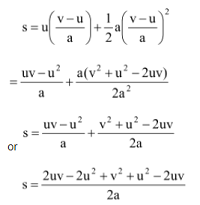
or v 2 = u 2 + 2as
or v 2 - u 2 = 2as
This is the third equation of motion
Where v = final velocity
u = initial velocity
a = acceleration
s = distance traveled
Distance covered in nth second :
S = ut + 1/2 at 2 is the distance covered by a body in t s.
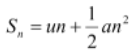 ........(v)
........(v)
[distance covered by a body along a straight line in n second.
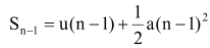 .......(vi)
.......(vi)
[distance covered by a body along a straight line in (n-1) sec.]
The distance covered by the body in nth second will be -
S n th = S n – S n -1
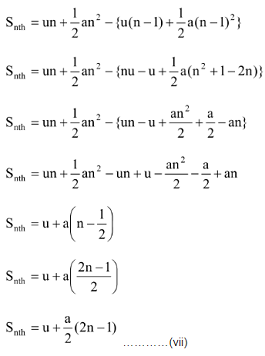
To Solve Numerical problems:
- If a body is dropped from a height then its initial velocity u = 0 but has acceleration (acting). If a body starts from rest its initial velocity u = 0.
- If a body comes to rest, its final velocity v = 0 or, if a body reached the highest point after being thrown upwards its final velocity v = 0 but has acceleration (acting).
- If a body moves with uniform velocity, its acceleration is zero i.e. a = 0.
- Motion of body is called free fall if only force acting on it is gravity (i.e. earth’s attraction).
MOTION UNDER GRAVITY
- Motion under gravity means an object is in motion in space under the force of gravity alone.
- Motion under gravity is a uniformly accelerated motion. So equations of motion for uniformly accelerated motion can be used which are
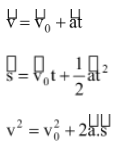
- Here acceleration will be acceleration due to gravity.
In SI-unit g = 9.8 m/s 2
In c.g.s. unit g = 980 cm/s 2
- When an object is thrown upward or downward, in both cases same acceleration ‘g’ will be experienced by the object, which acts in downward direction.
- Here air resistance is neglected. In a real experiment air resistance cannot be neglected. It is an ideal case. Such motion is referred to as free fall.
Case 1:
When an object is thrown in upward direction (taking positive) in space with initial velocity v0.
Acceleration = –g (in downward direction)
So, equation of motion will be
v = v 0 –gt
h = v 0 t – 1/2 gt2
v2 – 2gh
Case 2:
When an object is thrown in a downward direction (taking positive) in space with initial velocity v0.
Acceleration = +g (in downward direction)
So, equation of motion will be
v = v 0 +gt
s = v 0 t + 1/2 gt2
v 2 = v 0 2 + 2gh
|
Case 3: When an object is thrown in space in such a way that at first it goes up and then comes down. To solve such types of problem, the following sign convention is used:- Sign Convention Motional quantities in upward-direction are taken as positive. Motional quantities, which are in downward-direction, are taken as negative. |
|
Let initial velocity is v 0 which is in vertically upward direction and finally comes down to the ground as shown in figure.
Initial velocity = +v 0 (in upward directions)
Displacement = –h (in downward direction)
Acceleration = –g (in downward direction)
So using equation of motion, s =
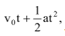 we have
we have
– h = v 2
Q1. A car is moving at a speed of 50 km/h. Two seconds thereafter it is moving at 60 km/h. Calculate the acceleration of the car.
Ans. Here u = 50 km/h = 50 × 5/18 m/s = 250/18 m/s
and v = 60 km/h = 60 × 5/18 = 300/18 m/s
Since a
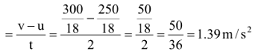
Q2 . A car attains 54 km/h in 20 s after it starts. Find the acceleration of the car.
Ans. u = 0 (as car starts from rest)
v = 54 km/h = 54 × 5/18 = 15 m/s
As,
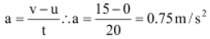
Q 3. A ball is thrown vertically upwards with a velocity of 20 m/s. How high did the ball go? (take g = 9.8 m/s2.
Ans. u = 20 m/s, a = - g = - 9.8 m/s2 (moving against gravity)
s = ? v = 0 (at highest point)
v 2 – u 2 = 2as
(o)2 – (20)2 = 2(-g) s
–400 = 2 (–9.8) s
–400 = –19.6 s
= s ⇒ s = 20.4 m.
DISTANCE (DISPLACEMENT) FROM SPEED (VELOCITY) TIME GRAPH:
A distance (displacement = speed (velocity) x time, so the distance (displacement) can be calculated (computed) with speed (velocity) - time graph.
Case (i): When speed (velocity) is uniform (constant):
Figure shows the speed - time graph of a car moving with a uniform speed of 50 km h-1. It is a straight line parallel to X - axis (time axis). Distance covered by this taxi from time t1 = 4h at P to time t2 = 8 h at S, is given by distance = 50 × (t 2 - t 1 )
= 50 (8 - 4)
= 50 × 4 = 200 km
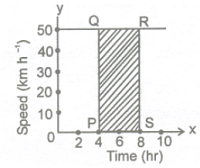
In figure, PQ = 50, SP = (t 1 - t 1 )
Hence distance = PQ × SP = Area of rectangle PSRQ
Case (ii) : When speed (velocity) as well as acceleration is non-uniform (variable)
Figure shows the speed- time graph of a body moving with variable speed and acceleration. Over a small interval of time, the speed can be taken as constant. For this small time interval, distance ΔS = vΔt = Area of the blackened strip.
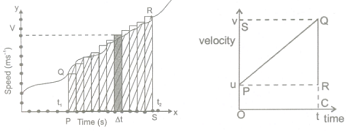
For whole time-interval between t 1 and t 2
Distance = sum of area of all the strips between t 1 and t 2 = Area of shaded figure PQRS.
GRAPHICAL DERIVATION OF EQUATIONS OF MOTION
TO DERIVE v = u + at BY GRAPHICAL METHOD
Let us consider a body moving with uniform acceleration ‘a’ having initial velocity ‘u’ attains the final velocity v in time ‘t’ covering a distance ‘s’ as shown in the graph.
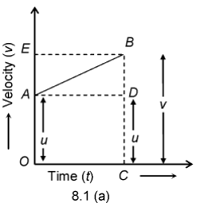
In the given velocity time graph,
Initial velocity, u = OA …(i)
Final velocity, v =BC …(ii)
From the graph, BC = BD + DC
⇒ v = BD + OA(DC = OA)
⇒ v = BD + u …(iii)
To find the value of BD,
Acceleration, a = slope of line AB
or a = BD/AD
⇒ a = BD/t (AD = OC = t)
⇒ BD = at …(iv)
Putting BD = at in equation (iii)
We get v = at + u
or v = u + at
TO DERIVE S = ut + 1/2at 2 BY GRAPHICAL METHOD
Let us consider a body moving with uniform acceleration ‘a’ having initial velocity ‘u’ attains the final velocity ‘v’ in time ‘t’ covering a distance s as shown in the graph 8.1 (a).
Then from the graph:
Distance travelled by the body = Area under the velocity time graph
Distance travelled = Area of figure OABC = area of rectangle OADC + Area of triangle ABD
⇒ S = (OA x OC) + (1/2 AD x BD)
⇒ S = u x t + 1/2t x BD …(i)
To find the value of BD,
Acceleration, a= slope of line AB
or a = BD/AD
⇒ a = BD/t (AD = OC = t)
⇒ BD = at
Putting BD = at in equation (i) we get
S = ut + 1/2at 2
TO DERIVE v 2 - u 2 = 2as BY GRAPHICAL METHOD
Let us consider a body moving with uniform acceleration ‘a’ having initial velocity ‘u’ attains the final velocity ‘v’. In time ‘t’ covering a distance s as shown in the graph 8.1 (a).
Then from the graph:
Distance travelled, 's' = area under the velocity time graph
i.e. Distance travelled, s= area of trapezium OABC
sum of parallel sides x height/2
= (OA + CD) x OC/2
s = (u + v) x t/2….(i)
To eliminate ‘t’ from the above equation
We know, v = u + at
⇒ v - u = at
⇒ t = (v - u/a)…(ii)
By putting this value in equation (i),
We get, s = (u + v)(v-u)/2a
⇒ v 2 = u 2 + 2as
⇒ v 2 - u 2 = 2as
- Slope of distance-time/displacement-time graph gives speed/velocity.
- Slope of speed-time/velocity-time graph gives acceleration.
- Area under speed-time/velocity-time graph gives distance/displacement.
- Area under acceleration-time graph gives change in velocity.
CIRCULAR MOTION:
Definition:
Motion of a particle (small body) along a circle (circular path), is called a circular motion. If the body covers equal distances along the circumference of the circle in equal intervals of time, the motion is said to be a uniform circular motion.
A uniform circular motion is a motion in which speed remains constant but direction of velocity changes.
Explanation:
Consider a boy running along a regular hexagonal track (path) as shown in figure. As the boy runs along the side of the hexagon at a uniform speed, he has to take turn at each corner changing direction but keeping the sped same. In one round he has to take six turns at regular intervals.
If the same boy runs along the side of a regular octagonal track with same uniform speed, he will have to take eight turns in one round at regular intervals but the interval will become smaller.
By increasing the number of sides of the regular polygon, we find the number of turns per round becomes more and the interval between two turns become still shorter. A circle is a limiting case of polygon with an infinite number of sides. On the circular track, the turning becomes a continuous process without any gap in between.

The boy running along the sides of such a track will be performing a circular motion. Hence, circular motion is the motion of a body along the sides of polygon of infinite number of sides with uniform speed, the direction changing continuously.
Example of uniform circular motion are:
- Motion of moon around the earth.
- Motion of satellite around its planet.
Nature of Circular of Motion:
Circular motion is an acceleration motion. Since, in a circular motion, velocity changes though in direction only, the motion is said to be accelerated.
DIFFERENCE BETWEEN UNIFORM LINEAR MOTION AND A UNIFOR CIRCULAR MOTION:
|
Uniform linear motion |
Uniform circular motion |
|
1. The direction of motion does not changes |
1. The direction of motion changes continuously. |
|
2. The motion is non-accelerated. |
2. The motion is accelerated. |
RADIAN - (A UNIT FOR PLANE ANGLE):
Definition:
An angle in radian is equal to the length of the arc subtending the angle divided by the radius of the circle.
i.e.
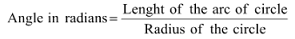
i.e. θ (in radians) = l/r
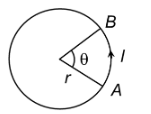
Where θ = angle in radians
l = length of the arc
r = radius of the circle
if l = r
∴ θ = l/l = 1 radian
i.e. θ = 1 radian
Therefore, one radian is that angle that is subtended at the center of a circle by an arc having a length equal to the radius of the circle.
(1 radian = 57°2616)
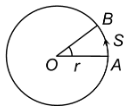
LINEAR SPEED AND ANGULAR VELOCITY:
|
Let a body is moving in a circular path of radius ‘r’ with a uniform linear speed ‘v’ when the body moves from point A to point B covering a distance ‘s’ in time ‘t’. Then the linear speed v is given by: |
|
Linear speed = Distance traveled/TIme taken
i.e. v = s/t
When the body moves on the circular path from A to B in time t. It also moves through an angle θ, which is known as the angular displacement of the body.
ANGULAR VELOCITY:
It is defined as the angular displacement per unit time
i.e. Angular velocity = Angular displacement / time taken
or (Omega)
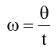
where ω = angular velocity
θ = Angle in radian, through which the body moves.
S.I. unit of angular velocity is rad s1.
RELATION BETWEEN LINEAR SPEED AND ANGULAR VELOCITY:
When a body is moving with uniform linear speed ‘v’ covering a distance ‘s’ in time ‘t’ on a circular path of radius ‘r’, subtending an angle θ at the center.
Then we have
Angle in radian, θ = s/r …(i)
And Linear speed v = s/t
s = v x t
Putting this in equation (i)
We have
θ = v x t/r
θ/t = v/r…(ii)
We know, Angular velocity,
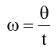
Putting this in equation (ii)
We get (ω) = v/r
v = ωr
i.e. Linear speed = Angular velocity × Radius of the circular path
Also Check