
Quadratic Equation
Quadratic Equations of Class 10
A polynomial of degree 2 (i.e.ax 2 + bx + c) is called a quadratic polynomial where a ≠ 0 and a, b, c are real numbers.
GENERAL FORM OF A QUADRATIC EQUATION:
The general form of quadratic equation is ax 2 + bx + c = 0, where a,b,c are real numbers and a ≠ 0 Since a ≠ 0, quadratic equations, in general are of the following types :-
(i) b = 0, c ≠ 0i.e., of the type ax 2 + c = 0.
(ii) b ≠ 0c = 0, i.e. of the type ax 2 + bx = 0.
(iii) b = 0, c = 0, i.e. of the type ax 2 = 0.
(iv) b ≠ 0, c ≠ 0i.e., of the type ax 2 + bx + c = 0.
CLASSIFICATION OF A QUADRATIC EQUATION:
It is classified into two categories:
(i) Pure quadratic equation (of the form ax 2 + c = 0 i.e., b = 0 in ax 2 + bx + c)
e.g. x 2 - 4 = 0 and 3x 2 + 1 = 0 are pure quadratic equations.
(ii) Affected quadratic equation (of the form ax 2 + bx + c = 0, b ≠ 0).
e.g. x 2 - 2x - 8 = 0 and 5x 2 + 3x - 2 = 0 are affected quadratic equations.
ZEROS OF QUADRATIC POLYNOMIAL:
For a quadratic polynomial p(x) = ax 2 + bx + c, those values of x for which ax 2 + bx + c = 0 is satisfied, are called zeros of quadratic polynomial p(x), i.e. if p(α) = aα 2 + bα + c = 0 then α is called the zero of quadratic polynomial.
ROOTS OF A QUADRATIC EQUATION:
The value of x which satisfies the given quadratic equation is known as its root. The roots of the given equation are known as its solution.
General form of a quadratic equation is :
ax 2 + bx + c = 0
or 4a 2 x 2 + 4abx + 4ac = 0 [Multiplying by 4a]
or 4a 2 x 2 + 4abx = –4ac [By adding b 2 both sides]
or 4a 2 x 2 + 4abc + b 2 = b 2 – 4ac
or (2ax + b) 2 = b 2 – 4ac
Taking square root of both the sides
2ax + b =
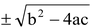
or
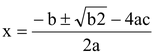
Hence, roots of the quadratic equation ax2 + bx + c = 0 are
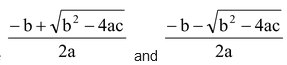
REMARK:
A quadratic equation is satisfied by exactly two values of ‘a’ which may be real or imaginary. The equation, ax2 + bx + c = 0 is :
- A quadratic equation if a ≠ 0 Two roots
- A linear equation if a = 0, b ≠ 0 One root
- A contradiction if a = b = 0, c ≠ 0 No root
- An identify if a = b = c = 0 Infinite roots
- A quadratic equation cannot have more than two roots.
- If follows from the above statement that if a quadratic equation is satisfied by more than two values of x, then it is satisfied by every value of x and so it is an identity.
NATURE OF ROOTS :
Consider the quadratic equation, ax 2 + bx + c = 0 having αβ as its roots and b 2 – 4ac is called discriminate of roots of quadratic equation. It is denoted by D or Δ.
Roots of the given quadratic equation may be
(i) Real and unequal (ii) Real and equal (iii) Imaginary and unequal.
Let the roots of the quadratic equation ax2 + bx + c = 0 (where a ≠ 0,b,c ∈ R ) be α and β then
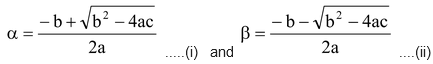
The nature of roots depends upon the value of expression ‘b2 - 4ac’ within the square root sign. This is known as discriminate of the given quadratic equation.
Consider the Following Cases:
Case-1 When b 2 - 4ac > 0, (D > 0)
In this case roots of the given equation are real and distinct and are as follows
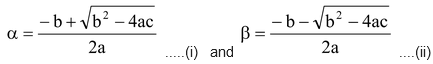
(i) When a ≠ 0,b,c ∈ Q and b 2 - 4ac is a perfect square
In this case both the roots are rational and distinct.
(ii) When a ≠ 0,b,c ∈ Q and b 2 - 4ac is not a perfect square
In this case both the roots are irrational and distinct. [See remarks also]
Case-2 When b 2 - 4ac = 0, (D = 0)
In this case both the roots are real and equal to -b/2a.
Case-3 When b 2 - 4ac < 0, (D < 0)
In this case b 2 – 4ac < 0, then 4ac – b 2 > 0
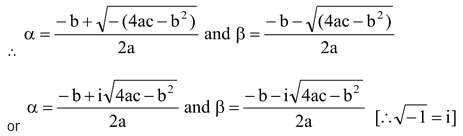
i.e. in this case both the root are imaginary and distinct.
REMARKS:
- If a,b,c ∈ Q and b2 - 4ac is positive (D > 0) but not a perfect square, then the roots are irrational and they always occur in conjugate pairs like 2 + √3 and 2- √3. However, if a, b, c are irrational number and b2 – 4ac is positive but not a perfect square, then the roots may not occur in conjugate pairs.
- If 2 – 4ac is negative (D > 0), then the roots are complex conjugate of each other. In fact, complex roots of an equation with real coefficients always occur in conjugate pairs like 2 + 3i and 2 – 3i. However, this may not be true in case of equations with complex coefficients. For example, x2 – 2ix – 1 = 0 has both roots equal to i.
- If a and c are of the same sign and b has a sign opposite to that of a as well as c, then both the roots are positive, the sum as well as the product of roots is positive (D ≥ 0).
- If a,b, are of the same sign then both the roots are negative, the sum of the roots is negative but the product of roots is positive (D ≥ 0).
question 1. Check whether the following equations are quadratic or not.
(i)
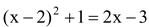 (ii)
(ii)
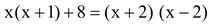
(iii)
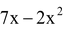 (iv)
(iv)
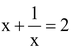
Solution:
(i)
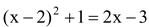 can be rewritten as
can be rewritten as
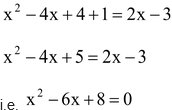
It is of the form ax 2 + bx + c = 0
Therefore, the given equation is a quadratic equation.
(ii) As
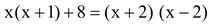 and (x + 2) (x - 2) = x
2
- 4
and (x + 2) (x - 2) = x
2
- 4
Therefore, we have x 2 + x + 8 = x 2 - 4
⇒ x + 12 = 0
It is not of the form ax 2 + bx + c = 0
Therefore, the given equation is not a quadratic equation.
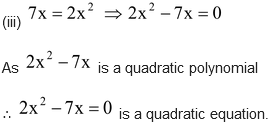
(iv)
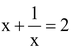
⇒ x + x -1 - 2 = 0
Since x + x -1 - 2 is not a quadratic polynomial.
∴
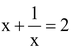 is not a quadratic equation
is not a quadratic equation
question 2. In each of the following, determine the value of k for which the given value is a solution of the equation.
(i)
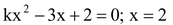
(ii)
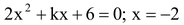
Solution:
(i)
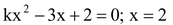 …(i)
…(i)
Since x = 2 is a solution of the equation
Now substituting x = 2 in equation (i), we get
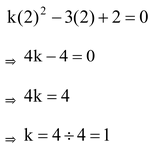
(ii) Since x = –2 is a solution of the equation
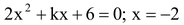 …(i)
…(i)
Now substituting x = – 2 in (i), we get
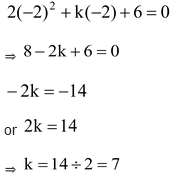
Do solve NCERT text book for class 10 maths with the help of pw NCERT solutions for class 10 maths.




