
Quadratic Expressions
Quadratic equation of Class 11
Quadratic Expressions
Let F(x) = ax 2 + bx + c, a,b,c ∈ R, a ≠ 0.
The graph of f (x) is a parabola with vertex at
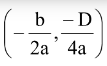 .
.
The mouth of the parabola opens up or down according as 'a' is positive or negative respectively.
Three cases arise
(i) If D < 0, aF(x) > 0 for all values of x.
(ii) If D = 0, F(x) = 0 has two equal roots and aF(x) ≥ 0.
(iii) If D > 0, F(x) = 0 has two real and distinct roots say α and β. Let α< β.
In this case a F(x) < 0 for all x ∈ (α, β), a F(α) = 0, a F(β) = 0 and
a F(x) > 0 ∀ x ∈ (−∞, α) ∪ (β, ∞).
(iv) If D ≥ 0, a F(k) > 0 for any real number k and -
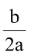 > k. Then both the roots of
> k. Then both the roots of
F(x) = 0 are greater than k.
(v) If D ≥ 0, a F(k) > 0 and −
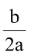 < k for any real number k, then both the roots are smaller than k.
< k for any real number k, then both the roots are smaller than k.
(vi) If D > 0 and a F(k) < 0 for any real number k, then k lies between the roots of
F(x) = 0.
(vii) Exactly one root of F(x) = 0 lies between the real numbers k1 and k2 if
F(k1) F(k
2
) < 0.









