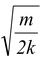The Spring-Mass System
Simple Harmonic Motion of Class 11
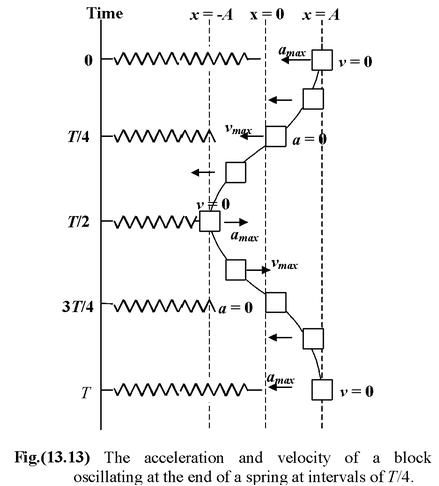
Let us find out the time period of a spring-mass system oscillating on a smooth horizontal surface as shown in the figure(13.6).
At the equilibrium position the spring is relaxed. When the block is displaced through a distance x towards right, it experiences a net restoring force F = -kx towards left.
|
The negative sign shows that the restoring force is always opposite to the displacement. That is, when x is positive, F is negative, the force is directed to the left. When x is negative, F is positive, the force is directed to the right. Thus, the force always tends to restore the block to its equilibrium position x = 0. F = -kx Applying Newton’s Second Law,
F = m
or
|
|
Comparing the above equation with (13.10), we get
ω 2 = k/m
or T = 2π√m/k (13.13)
Note : That the time period is independent of the amplitude. For a given spring constant, the period increases with the mass of the block – a more massive block oscillates more slowly. For a given block, the period decreases as k increases. A stiffer spring produces quicker oscillations.
|
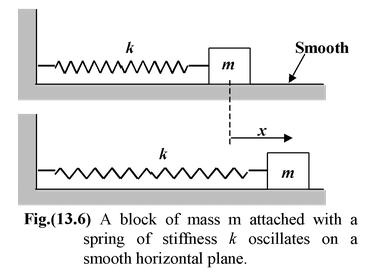
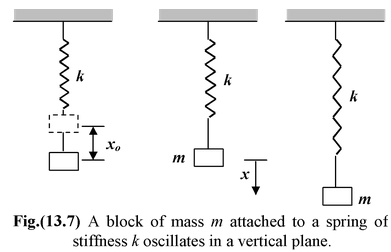
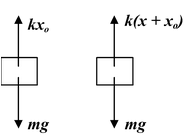
Example: 13.2 Find the period of oscillation of a vertical spring-mass system. Solution Let x o be the deformation in the spring in equilibrium. Then k xo = mg When the block is further displaced by x, the net restoring force is given by F = -[k(x + xo) – mg] orF = −kx (because k xo = mg) Using second law of motion,
m
or
|
|
Thus,ω 2 = k/m or T = 2π √m/k
Note that gravity does not influence the time period of the spring-mass system, it merely changes the equilibrium position.
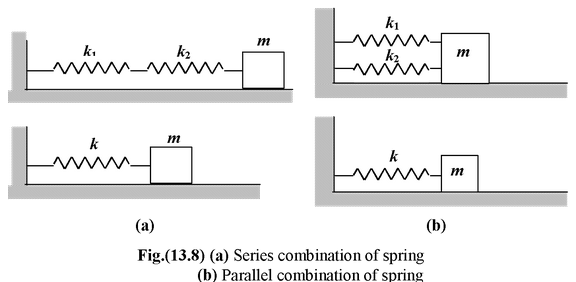
Series and Parallel Combinations of Springs
When two springs are joined in series, the equivalent stiffness of the combination may be obtained as
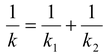 (13.14)
(13.14)
When two springs are joined in parallel, the equivalent stiffness of the combination is given by
k = k 1 + k 2 (13.15)
|
|
||
|
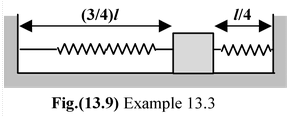
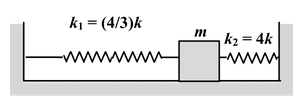
Example: 13.3 A spring of stiffness constant k and natural length l is cut into two parts of length and respectively , and an arrangement is made as shown in the figure . If the mass is slightly displaced, find the time period of oscillation. |
|
|
Solution
|
The stiffness of a spring is inversely proportional to its length. Therefore he stiffness of each part is k1 = 4/3k and k 2 = 4k
Time period , T =
or T =
|
|
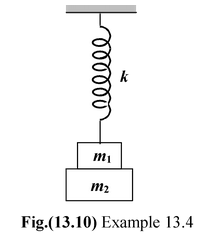
Example: 13.4Two masses m 1 and m 2 are suspended together by a massless spring of spring constant k. When the masses are in equilibrium m 1 is removed without disturbing the system. Find the angular frequency and amplitude of oscillation of m 2 . |
|
Solution
As m 1 is removed, the mass m 2 will oscillate and so
T = 2π
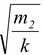 , i.e., ω =
, i.e., ω =
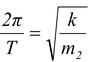
Furthermore, the stretch produced by m1g will set the amplitude,
i.e.m1g = kA i.e.A = (m1g/k)
Example: 13.5
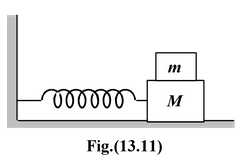
A horizontal spring block system of (force constant k) and mass M executes SHM with amplitude A. When the block is passing through its equilibrium position an object of mass m is put on it and the two move together. Find the new amplitude and frequency of vibration.
Solution
As initially mass M and finally (m + M) is oscillating,
f =
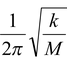 and f ′ =
and f ′ =
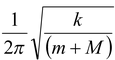
|
so that
i.e.f ′ = f
Now by conservation of linear momentum, Mv = (m + M)V |
|
and as at equilibrium position
v = Aω = 2πAf(as ω = 2πf)
M 2 πfA = (m + M) 2 πf′A′
i.e.
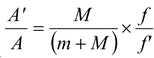
Using equation (i)
A′ = A
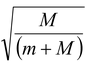
|
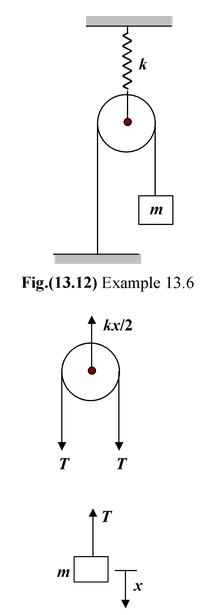
Example: 13.6 For the arrangement shown in the figure, find the period of oscillation. Solution Obviously, when the block displaced down by x, the spring will stretch by x/2 . From the free body diagram of the pulley, kx/2 = 2T or T = kx/4 The net restoring force on the block is T. Using the Second Law of motion, we get
Thus, the period of SHM is given by T = 2π√4m/k Note that we have not taken gravity into account as it does not affect the time period. |
|
Example: 13.7
A 2 kg block is attached to a spring for which k = 200 N/m. It is held at an extension of 5 cm and then released at t = 0. Find
(a)the displacement as a function of time
(b)the velocity when x = +A/2;
(c)the acceleration when x = +A/2, where A is the amplitude.
Solution
(a)We need to find a, ω, and φ in equation. The amplitude is the maximum extension; that is,
A = 0.05 m
We know the angular frequency of the spring-mass system is given by
ω = √k/m = 10 rad/s
To find φ we note that at t = 0 we are given x = +A and v = 0.
Thus, from the equation of displacement and velocity, we get
x = A sin (ω t + φ ) ⇒A = A sin (0 + φ)
v = ω A cos (ω t + φ) ⇒0 = 10 A cos (0 + φ)
Since sin φ = 1 and cos φ = 0, it follows that φ = π/2 rad. Thus,
x = 0.05 sin (10t + π/2) m (i)
(b)In order to find the velocity we have to find phase when x = A/2. Equation (i) yields
1/2 = sin(10t + π/2),
from which we get that (10 t + π/2) = π/6 or 5π/6
The velocity is given by
v = dx/dt = 0.5 cos (10t + π/2)
= 0.5 cos π/6 or 0.5 cos 5π/6
= +0.43 m/sor-0.43 m/s
At a given position, there are two velocities of equal magnitude but of opposite directions.
(c)The acceleration at x = A/2 may be found from the equation,
a =
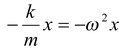 = -(10 rad/s)2(0.05/2 m) = -2.5 m/s
2
= -(10 rad/s)2(0.05/2 m) = -2.5 m/s
2
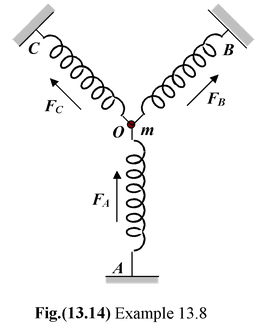
Example: 13.8
A particle of mass m is attached to three identical springs A, B and C each of force constant k as shown in figure. If the particle of mass k is pushed slightly against the spring A and released, find the time period of oscillations.
Solution
|
When the particle of mass m at O is pushed by y in the direction of A, spring A will be compressed by y while B and C will be stretched by y ′ = y cos 45o, so the total restoring force on the mass m along OA is given by F = −[FA + FBcos 45 o + FC cos 45 o ] i.e.F = − [ky + 2(ky′) cos 45] orF = − [ky + 2k(y cos 45) cos 45] i.e.,F = −k′y where k′ = 2k
soT = 2π
|
|
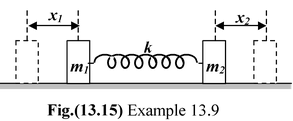
Example: 13.9
Two masses m 1 and m 2 are connected by a spring of force constant k and are placed on a frictionless horizontal surface. Show that if the masses are displaced slightly in opposite directions and released, the system will execute simple harmonic motion. Calculate the frequency of oscillation.
|
Solution Let masses m1 and m2 be displaced by x 1 and x 2 respectively from their equilibrium position in opposite direction so that the total extension in the spring will be x = x 1 + x 2 . Due to this stretch a restoring force kx will act on each mass and so equation of mass m1 will be |
|
m1
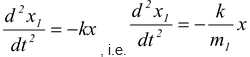 (i)
(i)
while that for m 2 will be
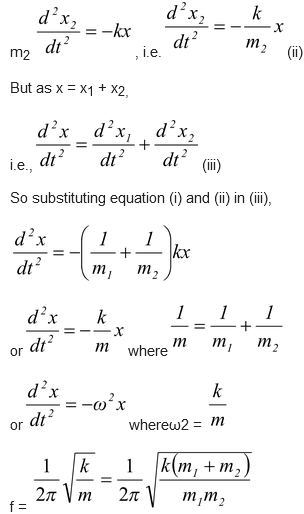
Example: 13.10
The angular displacement of simple pendulum is given by
θ = 0.1 π sin (2πt + π/6) rad
The mass of the bob is 0.4 kg. Calculate
(a)the length of the simple pendulum; and
(b)the velocity of the bob at t = 0.25 s
Solution
(a)We are given θo = 0.1 π rad, φ = π/6 rad, and ω = 2 π rad/s. Since ω2 = (g/L), we have
L =
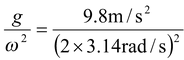 = 0.25 m
= 0.25 m
(b)Since s = Lθ, the velocity of the bob, v = ds/dt , is
v = L dθ/dt = (0.25 m)(0.1 π)(2π)cos (π/2 + π/6)
= −0.123 m/s

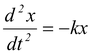
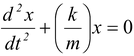
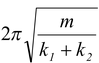
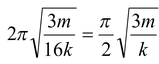
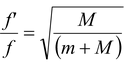
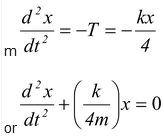
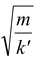 = 2π
= 2π