Stress, Strain and Elastic Modulii
Solids And Fluids of Class 11
Stress, Strain and Elastic Modulii
A force applied to an object can change its dimensions and shape. In general, the response of a material to a given type of deforming force is characterized by an elastic modulus, which is defined as
Elastic modulus = Stress/Strain (12.1)
The precise definition of stress depends on the particular situation being considered, but in general it is a force per unit area.
The strain indicates some fractional change in a dimension or volume. The unit of stress is N/m2, whereas strain is a dimensionless number.
Young’s Modulus
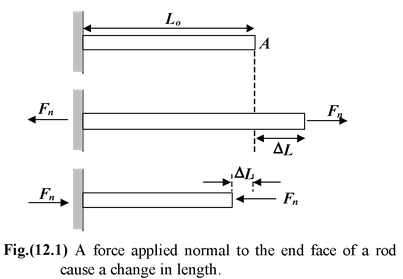
Young’s modulus is a measure of the resistance of a solid to a change in its length when a force is applied perpendicular to a face. Consider a rod with an unstressed length Lo and cross-sectional area A, as shown in the figure(12.1). When it is subjected to equal and opposite forces Fn along it axis and perpendicular to the end faces its length changes by ΔL. These forces tend to stretch the rod. The tensile stress on the rod is defined as
σ = F n /A (12.2)
Forces acting in the opposite direction, as shown in figure(12.1), would produce a compressive stress. The resulting strain is defined as the dimensionless ratio.
ε = ΔL/Lo (12.3)
|
Young’s modulus Y for the material of the rod is defined as the ratio of tensile stress to tensile strain. so Young’s Modulus = Tensile stress/Tensile strain
Y =
|
|
Example: 12.1
A metal wire 75 cm long and 0.139 cm in diameter stretches 0.035 cm when a load of 8.0 kg is hung on its end. Find the stress, the strain, and the Young’s modulus of the material of the wire.
Solution
Stress =
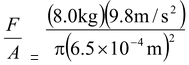 = 5.91 × 10
7
N/m
2
= 5.91 × 10
7
N/m
2
Strain =
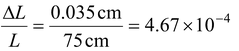
Y =
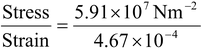 = 1.27 × 10
11
Nm
-2
= 1.27 × 10
11
Nm
-2
Example: 12.2
A solid cylindrical steel column is 4.0 m long and 9.0 cm in diameter. What will be its decrease in length when carrying a load of 80000 kg? Y = 1.9 × 1011 Nm-2.
Solution
Let us first calculate the cross-sectional area of column = πr 2 = π(0.045 m)2
= 6.36 × 10 -3 m 2
Then, from Y = (F/A)(ΔL/L) we have
ΔL =
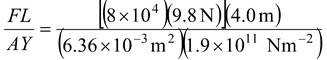 = 2.6 × 10-3 m = 2.6 mm
= 2.6 × 10-3 m = 2.6 mm
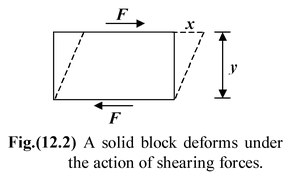
Shear Modulus
The shear modulus of a solid measures its resistance to a shearing force, which is a force applied tangentially to a surface, as shown in the figure (12.2). (Since the bottom of the solid is assumed to be at rest, there is an equal and opposite force on the lower surface.) The top surface is displaced by Δx relative to the bottom surface. The shear stress is defined as
Shear Stress = Tangetial Force/Area
T = F t /A (12.5)
where A is the area of the surface.
The shear strain is defined as
Shear strain = x/y (12.6)
|
where y is the separation between the top and the bottom surfaces. The shear modulus G is defined as Shear modulus = Shear Stress/Shear Strain
G =
|
|
Example: 12.3
A box shaped piece of gelatin dessert has a top area of 15 cm2 and a height of 3 cm. When a shearing force of 0.50 N is applied to the upper surface, the upper surface displaces 4 mm relative to the bottom surface. What are the shearing stress, the shearing strain, and the shear modulus for the gelatin?
Solution
Shear stress =
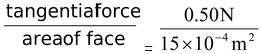 = 333 Pa
= 333 Pa
Shear strain =
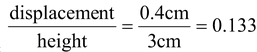
Shear modulus G =
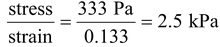
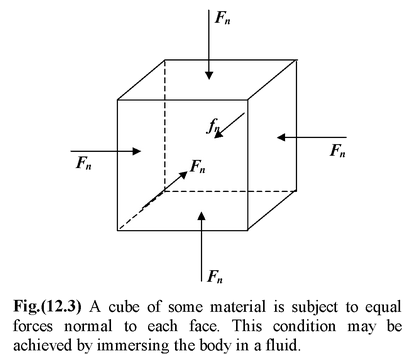
Bulk ModulusThe bulk modulus of a solid or a fluid indicates its resistance to a change in volume. Consider a cube of some material, solid or fluid, as shown in the figure. We assume that all faces experience the same force Fn normal to each face. (One way to accomplish this is to immerse the body in a fluid – as long as the change in pressure over the vertical height of the cube is negligible). The pressure on the cube is defined as the normal force per unit area |
|
p = F n /A (12.8)
The SI unit of pressure is N/m 2 and is given the name pascal (Pa).
Pressure is a scalar because on any infinitesimal volume, it acts in all directions; it has no unique direction.
When the pressure on a body is increased, its volume decreases. The change in pressure ΔP is called the volume stress and the fractional change in volume ΔV/V is called the volume strain. The bulk modulus B of the material is defined as
Bulk modulus = Volume stress/Volume strain
or B =
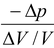 (12.9)
(12.9)
The negative sign is included to make B a positive number since an increase in pressure
(Δp > 0) leads to decrease in volume (ΔV < 0).
The inverse of B is called the compressibility,
k = 1/B(12.10)
Table 12.1 Elastic Properties of Matter
|
State |
Shear Modulus |
Bulk Modulus |
|
Solid |
Large |
Large |
|
Liquid |
Zero |
Large |
|
Gas |
Zero |
Small |

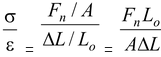 (12.4)
(12.4)
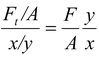 (12.7)
(12.7)