Surface Tension
Solids And Fluids of Class 11
Surface Tension
When a small quantity of water is poured on a clean glass plate, it spreads in all directions in the form of a thin film. But when a small quantity of mercury is poured on the glass plate, it takes the form of a spherical drop. Similarly, if a small quantity of water is poured on a greasy glass plate, it also takes the form of small globules like mercury. This shows that the behavior of liquids is controlled not only by gravitational force (weight) but some other force also acts upon it which depends upon the nature of the surfaces in contact. If the weight of the liquid is negligible then its shape is perfectly spherical. For example, rain drops and soap bubbles are perfectly spherical. We know that for a given volume, the surface area of sphere is least. Hence may say that the free surface of a liquid has a tendency to contract to a minimum possible area. This property of liquid is called surface tension.
Definition of Surface Tension
|
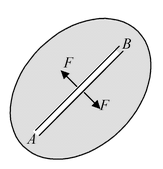
Let an imaginary line AB be drawn in any direction in a liquid surface. The surface on either side of this line exerts a pulling force on the surface on the other side. The force lies in the plane of the surface and is at right angles to the line AB. The magnitude of this force per unit length of AB is taken as a measure of the surface tension of the liquid. Thus if F be the total force acting on either side of the line AB of length l, then the surface tension is given by |
|
T = F/l
If l = 1 then T = F. Hence the surface tension of a liquid is defined as the force per unit length in the plane of the liquid surface, acting at right angles on either side of an imaginary line drawn in that surface. Its unit is Newton/meter and the dimensions
are [MT-2].
The value of the surface tension of a liquid depends on the temperature of the liquid, as well as on the medium on the other side of the surface. It decreases with rise in temperature and becomes zero at the critical temperature.
Surface Energy
When the surface area of a liquid is increased, the molecules from the interior rise to the surface. This requires work against the force of attraction of the molecules just below the surface. This work is stored in the form of potential energy in the newly formed surface. Besides this, there is cooling due to the increase in surface area. Therefore, heat flows into the surface from the surroundings to keep its temperature constant and is added to its energy. Thus the molecules in the surface have some additional energy due to their position. This additional energy per unit area of the surface is called surface energy.
Relation between Surface Tension and Work done in increasing the Surface Area:
|
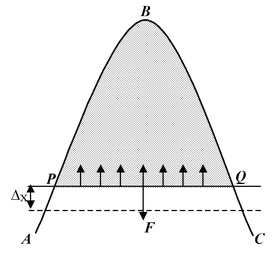
Let a liquid film be formed between a bent wire ABC and a straight wire PQ which can slide on the bent wire without friction. As the film surface tends to contract, the wire PQ moves upward. To keep PQ in equilibrium, a uniform force F (which includes the weight of the wire) has to be applied in the downward direction. |
|
It is found that the force F is directly proportional to the length l of the film in contact with the wire PQ. Since there are two free surfaces of the film, we have
F ∝ 2l or F = T × 2l
where T is a constant called ‘surface tension’ of the liquid. Now, suppose the wire is moved downward through a small distance Δx. This results in an increase in the surface area of the film. The work done by the force F(= force × distance) is given by
W = F × Δx = T × 2l × Δx
But 2l × Δx is the total increase in area of both the surfaces of the film. Let is be ΔA. Then
W = T × ΔA orT = W/ΔA
If ΔA = 1 then T = W. Then the work done in increasing the surface area by unity will be equal to the surface tension T. Hence, the surface tension of a liquid is equal to the work required to increase the surface area of the liquid film by unity at constant temperature. Therefore, surface tension may also be expressed in joule/meter2.
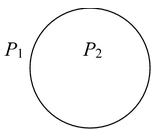
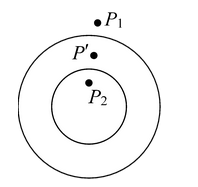
Excess pressure inside a dropLet us consider a spherical drop of liquid of radius R. If the drop is small, the effect of gravity may be neglected and shape may be assumed to be spherical. If the pressure just outside the surface is P1 and just inside the surface is P2. P 2 - P 1 = 2T/R The pressure inside the surface is greater than the pressure outside the surface. |
|
|
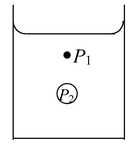
Note: The pressure on the concave side is greater than the pressure on the convex side. If there is an air bubble inside the liquid as shown in the figure, is single surface is formed. There is air on the concave side and liquid on the convex side. The pressure in the concave side is greater than the pressure in the convex side, by an amount 2T/R. |
|
P 2 - P 1 = 2T/R
Excess Pressure Inside a Soap Bubble
|
Let the pressure of the air outside the bubble be P1, within the soap solution be P′ and that in the air inside the bubble be P2. P′ - P 1 = 2T/R Similarly, looking at the inner surface, P 2 - P′ = 2T/R Adding these two equations, P 2 - P 1 = 4T/R |
|
Angle of Contact
When the free surface of a liquid comes in contact of a solid, it becomes curved near the place of contact. The angle inside the liquid between the tangent to the solid surface and the tangent to the liquid surface at the point of contact is called the angle of contact for that pair of solid and liquid.
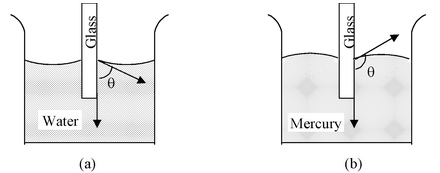
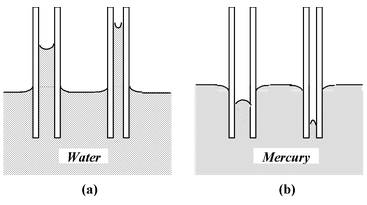
The angle of contact for those liquids which wet the solid is acute. It is zero for pure water and clean glass; for ordinary water and glass it is about 8o. The liquids which do not wet the solid have obtuse angle of contact. For mercury and glass the angle of contact is 135o. In figure (a) and (b) are shown the angles of contact θ for water-glass and mercury-glass.
The angle of contact for water and silver is 90o. Hence in a silver vessel the surface of water at the edges also remains horizontal.
Capillarity
|
When a glass capillary tube open at both ends is dipped vertically in water, the water rises up in the tube to a certain height above the water level outside the tube. The narrower the tube, the higher is the rise of water. On the other hand, if the tube is dipped in mercury, the mercury is depressed below the outside level. |
|
The phenomenon of rise or depression of liquids in a capillary tube is called capillarity. The liquids which wet glass (for which the angle of contact is acute) rise up in the capillary tube, while those which do not wet glass (for which the angle of contact is obtuse) are depressed down in the capillary.
|
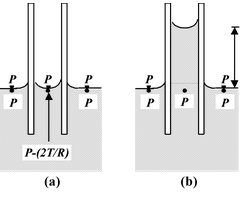
Explanation: The phenomenon of capillarity arises due to the surface tension of liquids. When a capillary tube is dipped in water, the water meniscus inside the tube is concave. The pressure just below the meniscus is less than the pressure just above it by 2T/R, where T is the surface tension of water and R is the radius of curvature of meniscus. |
|
The pressure of the surface of water is atmospheric pressure P. The pressure just below plane surface of water outside the tube is also P, but that just below the meniscus inside the tube is P – (2T/R). We know that pressure at all points in the same level of water must be the same.
Therefore, to make up the deficiency of pressure, 2T/R, below the meniscus, water begins to flow from outside into the tube. The rising force water in the capillary stops at a certain height h. In this position the pressure of the water-column of height h becomes equal to 2T/R, that is,
hρg = 2T/R
|
where ρ is the density of water and g is the acceleration due to gravity. If r be the radius of the capillary tube and θ the angle of contact of water-glass, then the radius of curvature R of the meniscus is given by
∴ hρg = 2T/r/cosθ or h = 2Tcos θ/rρg |
|
This shows that as r decreases, h increases, that is, narrower the tube, greater is the height to which the liquid rises in the tube.
Rising of liquid in a capillary tube of insufficient length:
Suppose a liquid of density ρ and surface tension T rises in a capillary tube to a height h.
Then hρg = 2T/R
where R is the radius of curvature of the liquid meniscus in the tube. From this we may write
hR = 2T/ρg = constant (for a given liquid)
When the length of the tube is greater than h, the liquid rises in the tube to a height so as to satisfy the above relation. But if the length of the tube is less than h, say h′, then the liquid rise up to the top of the tube and then spreads out until its radius of curvature R increases to R′, such that
h′R′ = hR = 2T/ρg
It is clear that liquid cannot emerge in the form of a fountain from the upper end of a short capillary tube.