Coordinate Geometry Formula Equations and Concept
Coordinate Geometry Formula : Coordinate geometry is a significant branch of mathematics that aids in representing geometric shapes within a two-dimensional plane and understanding their properties.
Sawat Sayyed8 Sept, 2023
Share
Coordinate Geometry Formula : Coordinates serve as essential markers on our planet, allowing us to easily pinpoint locations on the world map. The Earth's coordinate system comprises imaginary lines known as latitudes and longitudes. Starting points for this system are the zero degrees 'Greenwich Longitude' and the zero degrees 'Equator Latitude.' In a similar manner, when locating a point on a plane or a piece of paper, we utilize coordinate axes consisting of the horizontal x-axis and the vertical y-axis.
Coordinate geometry is the field that examines geometric shapes by plotting them on the coordinate axes. Various shapes, including straight lines, curves, circles, ellipses, hyperbolas, and polygons, can be accurately drawn and scaled on the coordinate axes. Furthermore, coordinate geometry facilitates algebraic calculations and the exploration of geometric figure properties through the use of the coordinate system.Introduction to Coordinate Geometry
Coordinate geometry is a significant branch of mathematics that aids in representing geometric shapes within a two-dimensional plane and understanding their properties. In this discussion, we will delve into the concept of the coordinate plane and point coordinates, aiming to establish a fundamental grasp of coordinate geometry.The Coordinate Plane
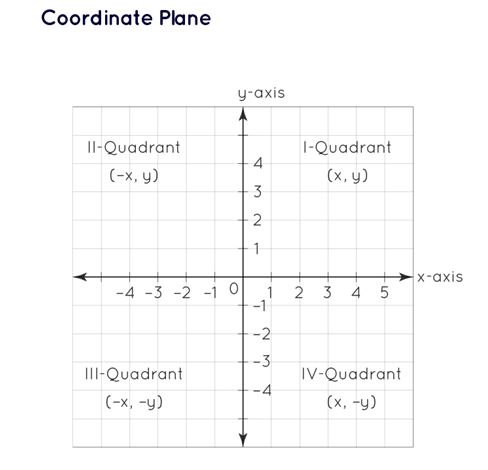
A Cartesian plane divides the plane's space into two dimensions, enabling the easy identification of points. This plane is also known as the coordinate plane and features two axes: the horizontal x-axis and the vertical y-axis. These axes partition the plane into four quadrants, with the intersection point being the origin (0, 0). Any point on the coordinate plane is designated by a pair of coordinates (x, y), where the x-coordinate represents the point's position along the x-axis, and the y-coordinate represents its position along the y-axis. Also Check - Rational Number Formula Key characteristics of points within the four quadrants are as follows:- The origin O, positioned at the intersection of the x-axis and y-axis, has coordinates (0, 0).
- To the right of the origin O, the x-axis is positive, and to the left, it is negative. Similarly, above the origin O, the y-axis is positive, while below it is negative.
- A point in the first quadrant (x, y) possesses positive values for both x and y and is situated relative to the positive x-axis and y-axis.
- In the second quadrant, a point (-x, y) is positioned with respect to the negative x-axis and positive y-axis.
- The third quadrant features a point (-x, -y), plotted relative to the negative x-axis and negative y-axis.
- The fourth quadrant hosts a point (x, -y), situated relative to the positive x-axis and negative y-axis.
Understanding the Coordinates of a Point
Coordinates function as location markers in space. For a two-dimensional space, a point's coordinates are expressed as (x, y). It is important to grasp two key terms associated with coordinates: Abscissa: In the point (x, y), the abscissa represents the x-value and denotes the point's distance along the x-axis from the origin. Ordinate: In the point (x, y), the ordinate signifies the y-value and indicates the perpendicular distance of the point from the x-axis, aligned parallel to the y-axis. Point coordinates prove valuable in various operations, including distance calculation, midpoint determination, slope computation, and line equation derivation. Topics Covered in Coordinate Geometry The topics within coordinate geometry lay the foundation for comprehending the concepts and formulas essential to this field. The covered subjects include:- Introduction to the coordinate plane and related terms.
- Understanding point coordinates and their representation across different quadrants.
- Formulas for calculating the distance between two points on the coordinate plane.
- Formulas for determining the slope of a line connecting two points.
- The midpoint formula for locating the midpoint of a line segment.
- The section formula for finding points that divide a line segment in a specific ratio.
- Determining the centroid of a triangle using its vertices on the coordinate plane.
- Calculating the area of a triangle with vertices in the coordinate geometry plane.
- Exploring the equation of a line and its various forms.
Also Check - Linear Equation Formula
Coordinate Geometry Formulas
Coordinate geometry formulas play a pivotal role in demonstrating the properties of lines and shapes represented on coordinate axes. These formulas encompass the distance formula, slope formula, midpoint formula, section formula, and line equation. Each formula serves a distinct purpose in coordinate geometry:Coordinate Geometry Distance Formula
Distance Formula: This formula computes the distance between two points (x1, y1) and (x2, y2) as the square root of the sum of squared differences in their x and y coordinates. Distance (D) = √ ( x 2 − x 1 ) 2 +( y 2 − y 1 ) 2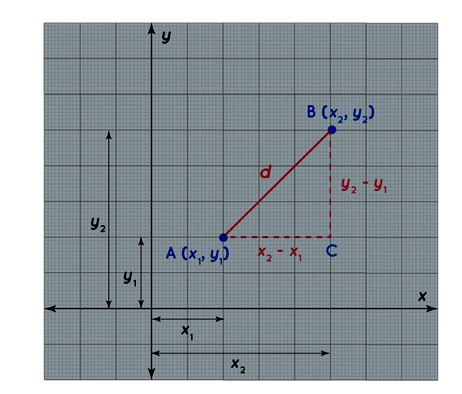
from the above figure:
By the Pythagoras’ theorem,
AB
2
= AC
2
+ BC
2
d
2
= (x
2
– x
1
)
2
+ (y
2
– y
1
)
2
Taking the square root on both sides,
d = √[(x
2
– x
1
)
2
+ (y
2
– y
1
)
2
]
This is called the distance between two points formula.
Also Check - Algebra Formulas
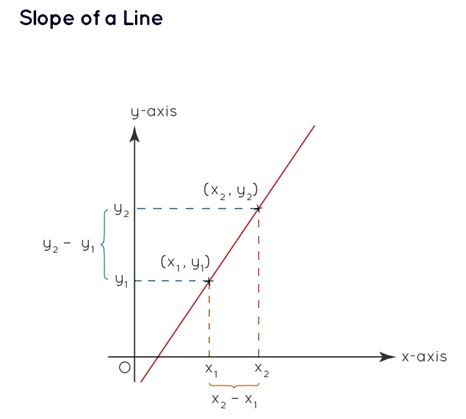
Coordinate Geometry Slope Formula
Slope Formula : The slope of a line can be calculated using the angle it forms with the positive x-axis or by selecting two points on the line. Slope (m) = Tanθ = (y2 - y1) / (x2 - x1)Finding Slope from a Graph
The slope of a line has only one value. So, the slopes found by Methods 1 and 2 will be equal. In addition to that, let's say we are given the equation of a straight line. The general equation can be given as, y = mx + b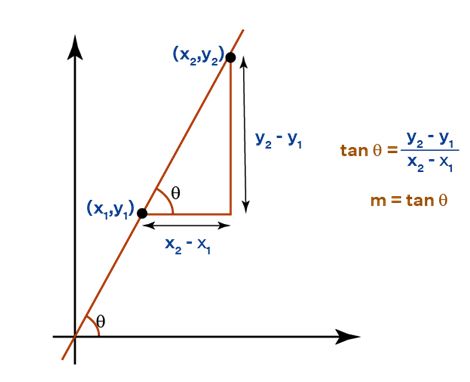
The value of the slope is given as
m;
hence the value of
m
gives the slope of any straight line.
The below-given steps can be followed to find the slope of a line such that the coordinates of two points lying on the line are: (2, 4), (1, 2)
- Step 1: Note the coordinates of the two points lying on the line, (x 2 , y 2 ), (x 1 , y 1 ). Here the coordinates are given as (2, 4), (1, 2).
- Step 2: Apply the slope of line formula, m = (y 2 - y 1 )/(x 2 - x 1 ) = (4 - 2)/(2 - 1) = 2.
- Step 3: Therefore, the slope of the given line = 2.
Coordinate Geometry Mid-Point Formula
Midpoint Formula: This formula determines the midpoint of a line joining two points (x1, y1) and (x2, y2). The midpoint's coordinates are the averages of the x and y coordinates of the given points.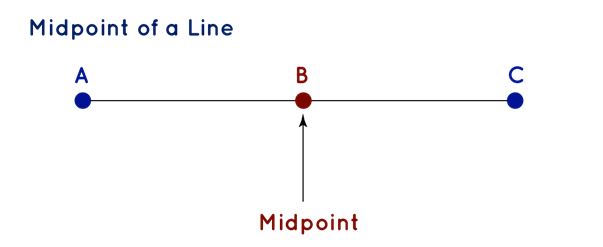
Given two points A (x
1
, y
1
) and B (x
2
, y
2
), the midpoint between A and B is given by,
M(x
3
, y
3
) = ((x
1
+ x
2
)/2, (y
1
+ y
2
)/2)
where, M is the midpoint between A and B, and (x
3
, y
3
) are its coordinates.
Midpoint (x, y) = ((x1 + x2) / 2, (y1 + y2) / 2)
Coordinate Geometry Section Formula
Section Formula: The section formula identifies the coordinates of a point that divides the line segment between two points (x1, y1) and (x2, y2) in a given ratio m:n.
Point (x, y) = ((mx2 + nx1) / (m + n), (my2 + ny1) / (m + n))
Coordinate Geometry Centroid Formula
Centroid Formula: The centroid of a triangle formed by vertices A (x1, y1), B (x2, y2), and C (x3, y3) can be found using the formula: Centroid (x, y) = ((x1 + x2 + x3) / 3, (y1 + y2 + y3) / 3)
Coordinate Geometry Area of a Triangle Formula
Area of a Triangle Formula: The area of a triangle with vertices A (x1, y1), B (x2, y2), and C (x3, y3) is computed using the formula: Area = 0.5 * |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|Determining the Equation of a Line in Coordinate Geometry
The equation of a line represents all points on the line through a linear equation. The standard form is ax + by + c = 0, where a, b, and c are constants. Several methods, including the slope-intercept form (y = mx + c), are used to find the equation. Other forms, such as the point-slope form, two-point form, intercept form, and normal form, provide additional perspectives on line equations. Coordinate geometry offers a powerful toolset for understanding and analyzing geometric shapes within a coordinate system. By utilizing these concepts and formulas, mathematicians and researchers can explore the intricate relationships between points, lines, and figures on a two-dimensional plane.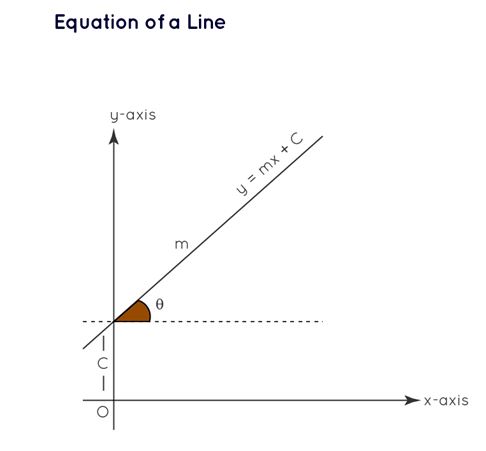
Points to Remember About Cartesian Coordinates
- The slope of the x-axis holds a value of 0, while the slope of the y-axis is considered infinite (∞).
- The x-axis is represented by the equation y = 0, and the y-axis is described by the equation x = 0.
- A point situated on the x-axis takes the form (a, 0), whereas a point located on the y-axis is represented as (0, b).
- The equation of a line in slope-intercept form is y = mx + c.
- In the coordinate plane, two lines that are parallel possess equal slopes.
- Furthermore, in the coordinate plane, when considering two perpendicular lines, the product of their slopes is equivalent to -1.
Coordinate Geometry Formula FAQs
Define the term Coordinate geometry.
Coordinate geometry is the field that examines geometric shapes by plotting them on the coordinate axes.
What is the meaning of the coordinate plane?
A Cartesian plane divides the plane's space into two dimensions, enabling the easy identification of points. This plane is also known as the coordinate plane and features two axes: the horizontal x-axis and the vertical y-axis.
What is the importance of Coordinate Geometry?
Coordinate geometry is of great importance in our life. It is used by us on a daily basis which includes:
GPS and Map Navigation use coordinate geometry to mark our location.
It used by the airline industry to plot the trajectory of a plane.
Explain the term Abscissa and Ordinates in Coordinate Geometry.
Abscissa: In the point (x, y), the abscissa represents the x-value and denotes the point's distance along the x-axis from the origin.
Ordinate: In the point (x, y), the ordinate signifies the y-value and indicates the perpendicular distance of the point from the x-axis, aligned parallel to the y-axis.
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
