NCERT Solutions for Class 10 Maths chapter-4 Quadratic Equations Exercise 4.4
Share
NCERT Solutions for Class 10 Maths chapter-4 Quadratic Equations Exercise 4.4
NCERT solutions for class-10 maths chapter 4 Quadratic Equations is prepared by academic team of Physics Wallah. We have prepared solutions for all exercises of this chapter. Given below is step by step NCERT solutions of all questions given in NCERT textbook for chapter 4. You have learned the formula of the given chapter 4 Quadratic Equations. Physics Wallah prepared a detail notes and additional questions for class-10 maths with short notes of all maths formula of class-10 maths.
NCERT Solutions for Class 10 Maths Exercise 4.4
Solve the followings Questions.
1. Find the nature of the roots of the following quadratic equation. If the real roots exist, find them:
Answer:
We know that the quadratic equation ax
2
+bx+c = 0 has
(a) Two distinct real roots, if b
2
-4ac > 0,
(b) Two equal real roots, if b
2
-4ac = 0,
(c) No real roots, if b
2
-4ac < 0.
(i) 2x
2
-3x+5 = 0
Answer:
Comparing the given quadratic equation with the general form of quadratic equation ax
2
+bx+c = 0 we get
a = 2, b = -3 and c = 5
Then, b
2
-4ac = (-3)
2
-4×2×5 = 9-40 = -31 < 0
Hence the given quadratic equation has no real roots.
(ii) 3x 2 -4√3x+4 = 0
Answer:
Comparing the given quadratic equation with the general form of quadratic equation ax
2
+bx+c = 0 we get
a = 3, b = -4√3 and c = 4
Then, b
2
-4ac = (-4√3)
2
-4×3×4 = 48-48 = 0
Therefore, real roots exist for the given equation and they are equal to each other.
And the roots will be
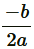
Therefore, the roots are
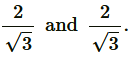
(iii) 2x 2 -6x+3 = 0
Answer:
Comparing the given quadratic equation with the general form of quadratic equation ax2+bx+c = 0 we get
a = 2, b = -6 and c = 3
then, b
2
-4ac = (-6)
2
-4×2×3 = 36-24 = 12 > 0
Hence the given quadratic equation has two distinct real roots.
Applying quadratic formula
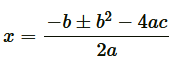to find roots,
2. Find the value of k for each of the following quadratic equations, so that they have two equal roots.
(i) 2x
2
+kx+3 = 0
Answer:
Comparing the given quadratic equation with the general form of quadratic equation ax
2
+bx+c = 0 we get
a = 2, b = k and c = 3
Now the given quadratic equation have two equal roots if
b
2
-4ac = 0
(k)2-4×2×3 = 0
k
2
-24 = 0
k
2
= 24
k = ±√24
k = ± 2√6
Therefore, the required value of k is ± 2√6.
(ii) kx(x-2)+6 = 0
Answer:
The given quadratic equation can be written as
kx
2
-2kx+6 = 0….(1)
Comparing the quadratic equation (1) with the general form of quadratic equation ax
2
+bx+c = 0 we get
a = k, b = -2k and c = 6
Now the given quadratic equation have two equal roots if
b
2
-4ac = 0
(-2k)
2
-4×k×6 = 0
4k
2
-24k = 0
4k(k-6) = 0
k(k-6) = 0
k = 0
Or, k-6 = 0
k = 6
If k = 0, then equation will not have x
2
and x, which is not possible because the given equation is quadratic equation.
Therefore, the required value of k is 6.
3. Is it possible to design a rectangular mango grove whose length is twice its breadth and the area is 800 m
2
. If so find its length and breadth.
Answer:
Let the breadth of the mango grove be x m and the length is 2x m.
Area = length × breadth
= x × 2x
= 2x2 m
2
Then by the given condition,
2x
2
= 800
x
2
= 400
x = ±√400
x = ±20
Since, length cannot be negative, then x ≠ -20
Hence it is possible to design a rectangular mango grove whose length is twice its breadth and the area is 800 m
2
and its breadth is 20 m and length is 20×2 = 40 m
4. Is the following situation possible? If so, determine their present ages .
The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
Answer:
Let the age of 1st friend is x.
Then the age of 2nd friend is (20-x)
Four year ago their age was (x-4) and (20-x-4)
Then using the given condition we have
(x-4)(16-x) = 48
16x – 64 – x
2
+4x = 48
20x – x
2
– 64 – 48 = 0
x
2
– 20x + 112 = 0……(1)
Now comparing the above quadratic equation with the general form of quadratic equation ax
2
+bx+c = 0 we get
a = 1, b = -20 and c = 112
then, b
2
-4ac = (-20)
2
-4×1×112 = 400-448 = -48 > 0
Therefore, no real root is possible for this equation and hence this situation is not possible.
5. Is it possible to design a rectangular park of perimeter 80 m and area 400 m
2
? If so find its length and breadth.
Answer:
Let the length and breadth of the park be “l” and “b”
Area of rectangle = 2(l + b)
2(l + b) = 80
l + b = 40
b = 40 – l
Then, Area = l(40 – l)
Then by the given condition,
l(40 – l) = 400
40l – l
2
-400 = 0
l
2
– 40l + 400 = 0….(1)
Now comparing the above quadratic equation with the general form of quadratic equation ax
2
+bx+c = 0 we get
a = 1, b = -40 and c = 400
Then, b
2
-4ac = (-40)
2
-4×1×400 = 1600-1600 = 0
As the quadratic equation has two equal roots then the given situation is possible.
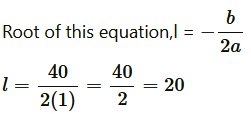
Therefore, length of park, l = 20 m
And breadth of park, b = 40 - l = 40 - 20 = 20 m.
