NCERT Solutions For Class 11 Maths chapter-11 Conic Sections Exercise 11.3
NCERT Solutions for Class-11 Maths Chapter-11 Conic Sections
NCERT Solutions for Class 11 Maths
Chapter-11 Conic Sections Exercise 11.3 is prepared by expert of Physics Wallah score more with Physics Wallah NCERT Class 11 maths solutions. You can download and share
NCERT Solutions
for Class 11 Maths.
NCERT Solutions for Class-11 Maths Exercise 11.3
In each of the Exercises 1 to 9, find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
Question 1.
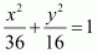
Solution :
The given equation is
.
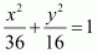Here, the denominator of
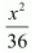is greater than the denominator of
.
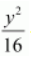Therefore, the major axis is along the
x
-axis, while the minor axis is along the
y
-axis.
On comparing the given equation with
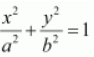, we obtain
a
= 6 and
b
= 4.
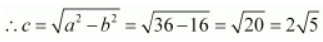
Therefore,
The coordinates of the foci are
.
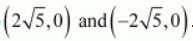The coordinates of the vertices are (6, 0) and (–6, 0).
Length of major axis = 2
a
= 12
Length of minor axis = 2
b
= 8
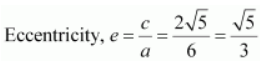
Length of latus rectum
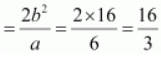
Question
2.
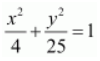
Solution :
The given equation is
.
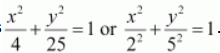Here, the denominator of
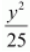is greater than the denominator of
.
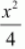Therefore, the major axis is along the
y
-axis, while the minor axis is along the
x
-axis.
On comparing the given equation with
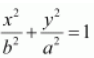, we obtain
b
= 2 and
a
= 5.
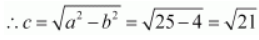
Therefore,
The coordinates of the foci are
.
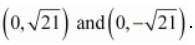The coordinates of the vertices are (0, 5) and (0, –5)
Length of major axis = 2
a
= 10
Length of minor axis = 2
b
= 4
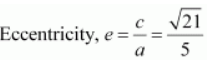
Length of latus rectum
Question 3.
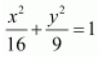
Solution :
The given equation is
.
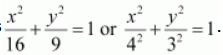Here, the denominator of
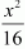is greater than the denominator of
.
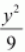Therefore, the major axis is along the
x
-axis, while the minor axis is along the
y
-axis.
On comparing the given equation with
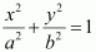, we obtain
a
= 4 and
b
= 3.
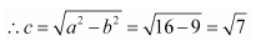
Therefore,
The coordinates of the foci are
.
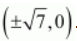The coordinates of the vertices are
.
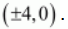Length of major axis = 2
a
= 8
Length of minor axis = 2
b
= 6
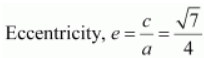
Length of latus rectum
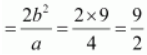
Question
4.
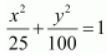
Solution :
The given equation is
.
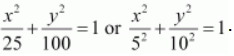Here, the denominator of
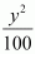is greater than the denominator of
.
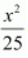Therefore, the major axis is along the
y
-axis, while the minor axis is along the
x
-axis.
On comparing the given equation with
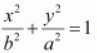, we obtain
b
= 5 and
a
= 10.
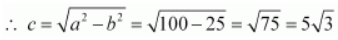
Therefore,
The coordinates of the foci are
.
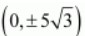The coordinates of the vertices are (0,
±
10).
Length of major axis = 2
a
= 20
Length of minor axis = 2
b
= 10
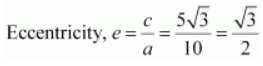
Length of latus rectum
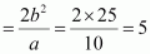
Question 5.
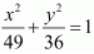
Solution :
The
given equation is
.
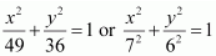Here, the denominator of
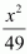is greater than the denominator of
.
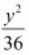Therefore, the major axis is along the
x
-axis, while the minor axis is along the
y
-axis.
On comparing the given equation with
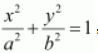, we obtain
a
= 7 and
b
= 6.
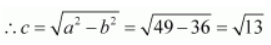
Therefore,
The coordinates of the foci are
.
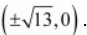The coordinates of the vertices are (
±
7, 0).
Length of major axis = 2
a
= 14
Length of minor axis = 2
b
= 12
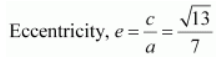
Length of latus rectum
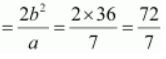
Question
6.
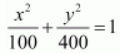
Solution :
The given equation is
.
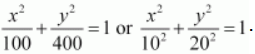Here, the denominator of
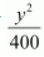is greater than the denominator of
.
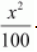Therefore, the major axis is along the
y
-axis, while the minor axis is along the
x
-axis.
On comparing the given equation with
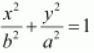, we obtain
b
= 10 and
a
= 20.
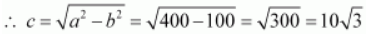
Therefore,
The coordinates of the foci are
.
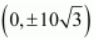The coordinates of the vertices are (0,
±
20)
Length of major axis = 2
a
= 40
Length of minor axis = 2
b
= 20
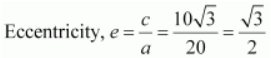
Length of latus rectum
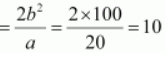
Question
7. Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 36x
2
+ 4y
2
= 144
Solution :
The given equation is 36x
2
+ 4y
2
= 144.
It can be written as
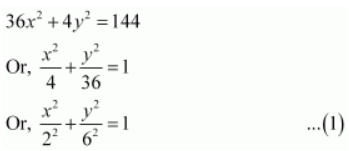
Here, the denominator of
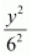is greater than the denominator of
.
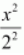Therefore, the major axis is along the
y
-axis, while the minor axis is along the
x
-axis.
On comparing equation (1) with
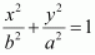, we obtain
b
= 2 and
a
= 6.
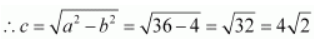
Therefore,
The coordinates of the foci are
.
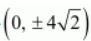The coordinates of the vertices are (0,
±
6).
Length of major axis = 2
a
= 12
Length of minor axis = 2
b
= 4
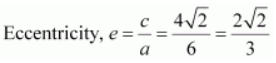
Length of latus rectum
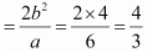
Question
8. Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 16x
2
+ y
2
= 16
Solution :
The given equation is 16
x
2
+
y
2
= 16.
It can be written as
Here, the denominator of
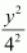is greater than the denominator of
.
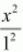Therefore, the major axis is along the
y
-axis, while the minor axis is along the
x
-axis.
On comparing equation (1) with
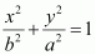, we obtain
b
= 1 and
a
= 4.
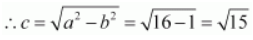
Therefore,
The coordinates of the foci are
.
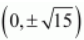The coordinates of the vertices are (0,
±
4).
Length of major axis = 2
a
= 8
Length of minor axis = 2
b
= 2
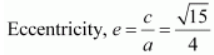
Length of latus rectum
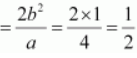
Question 9. Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 4x
2
+ 9y
2
= 36
Solution :
The given equation is 4
x
2
+ 9
y
2
= 36.
It can be written as
Here, the denominator of
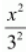is greater than the denominator of
.
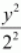Therefore, the major axis is along the
x
-axis, while the minor axis is along the
y
-axis.
On comparing the given equation with
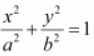, we obtain
a
= 3 and
b
= 2.
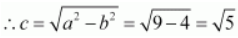
Therefore,
The coordinates of the foci are
.
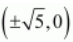The coordinates of the vertices are (
±
3, 0).
Length of major axis = 2
a
= 6
Length of minor axis = 2
b
= 4
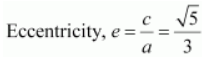
Length of latus rectum
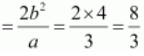
In each of the Exercises 10 to 20, find the equation of the ellipse that satisfies the given conditions:
Question 10. Find the equation for the ellipse that satisfies the given conditions: Vertices (±5, 0), foci (±4, 0)
Solution :
Vertices (±5, 0), foci (±4, 0)
Here, the vertices are on the x-axis.
Therefore, the equation of the ellipse will be of the form
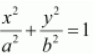, where a is the semi-major axis.
Accordingly, a = 5 and c = 4.
It is known that
.
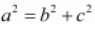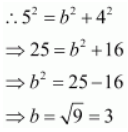
Thus, the equation of the ellipse is
.
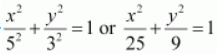Question
11. Find the equation for the ellipse that satisfies the given conditions: Vertices (0, ±13), foci (0, ±5)
Solution :
Vertices (0, ±13), foci (0, ±5)
Here, the vertices are on the
y
-axis.
Therefore, the equation of the ellipse will be of the form
,
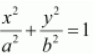where
a
is the semi-major axis.
Accordingly,
a
= 13 and
c
= 5.
It is known that
.
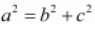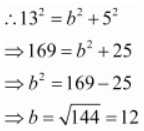
Thus, the equation of the ellipse is
.
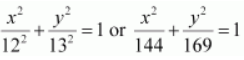Question
12. Find the equation for the ellipse that satisfies the given conditions: Vertices (±6, 0), foci (±4, 0)
Solution :
Vertices (±6, 0), foci (±4, 0)
Here, the vertices are on the
x
-axis.
Therefore, the equation of the ellipse will be of the form
,
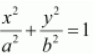where
a
is the semi-major axis.
Accordingly,
a
= 6,
c
= 4.
It is known that
.
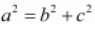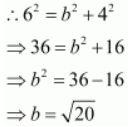
Thus, the equation of the ellipse is
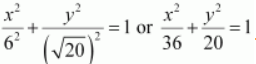
Question
13.Find the equation for the ellipse that satisfies the given conditions: Ends of major axis (±3, 0), ends of minor axis (0, ±2)
Solution :
Ends of major axis (±3, 0), ends of minor axis (0, ±2)
Here, the
major axis
is along the
x
-axis.
Therefore, the equation of the ellipse will be of the form
,
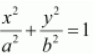where
a
is the semi-major axis.
Accordingly,
a
= 3 and
b
= 2.
Thus, the equation of the ellipse is
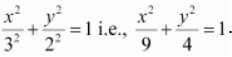
Question
14. Find the equation for the ellipse that satisfies the given conditions: Ends of major axis (0, ± √5), ends of minor axis (± 1, 0)
Solution :
Ends of major axis
(0, ± √5)
, ends of minor axis (±1, 0)
Here, the
major axis
is along the
y
-axis.
Therefore, the equation of the ellipse will be of the form
,
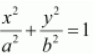where
a
is the semi-major axis.
Accordingly,
a
=
√
5
and
b
= 1.
Thus, the equation of the ellipse is
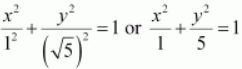
Question 15. Find the equation for the ellipse that satisfies the given conditions: Length of major axis 26, foci (± 5, 0)
Solution :
Length of major axis = 26; foci = (±5, 0).
Since the foci are on the
x
-axis, the
major axis
is along the
x
-axis.
Therefore, the equation of the ellipse will be of the form
,
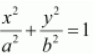where
a
is the semi-major axis.
Accordingly, 2
a
= 26
⇒
a
= 13 and
c
= 5.
It is known that
.
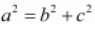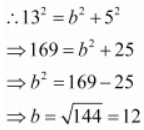
Thus, the equation of the ellipse is
.
.
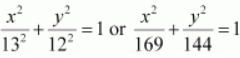Question 16. Find the equation for the ellipse that satisfies the given conditions: Length of minor axis 16, foci (0, ± 6).
Solution :
Length of minor axis = 16; foci = (0, ±6).
Since the foci are on the
y
-axis, the
major axis
is along the
y
-axis.
Therefore, the equation of the ellipse will be of the form
,
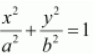where
a
is the semi-major axis.
Accordingly, 2
b
= 16
⇒
b
= 8 and
c
= 6.
It is known that
.
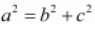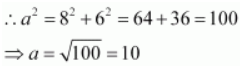
Thus, the equation of the ellipse is
.
.
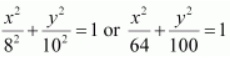Question 17. Find the equation for the ellipse that satisfies the given conditions: Foci (±3, 0), a = 4
Solution :
Foci (±3, 0),
a
= 4
Since the foci are on the
x
-axis, the
major axis
is along the
x
-axis.
Therefore, the equation of the ellipse will be of the form
,
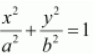where
a
is the semi-major axis.
Accordingly,
c
= 3 and
a
= 4.
It is known that
.
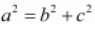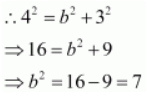
Thus, the equation of the ellipse is
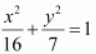
Question
18. Find the equation for the ellipse that satisfies the given conditions: b = 3, c = 4, centre at the origin; foci on the x axis.
Solution :
It is given that
b
= 3,
c
= 4, centre at the origin; foci on the
x
axis.
Since the foci are on the
x
-axis, the
major axis
is along the
x
-axis.
Therefore, the equation of the ellipse will be of the form
,
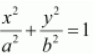where
a
is the semi-major axis.
Accordingly,
b
= 3,
c
= 4.
It is known that
.
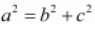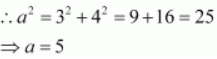
Thus, the equation of the ellipse is
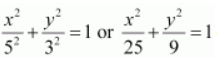
Question 19. Find the equation for the ellipse that satisfies the given conditions: Centre at (0,0), major axis on the y-axis and passes through the points (3, 2) and (1,6).
Solution :
Since the centre is at (0, 0) and the major axis is on the
y
-axis, the equation of the ellipse will be of the form
The ellipse passes through points (3, 2) and (1, 6). Hence,
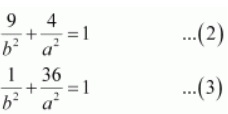
On solving equations (2) and (3), we obtain
b
2
= 10 and
a
2
= 40.
Thus, the equation of the ellipse is
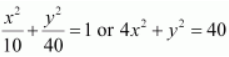
Question 20. Major axis on the x- axis and passes through the points (4, 3) and (6, 2).
Solution :
Since the major axis is on the
x
-axis, the equation of the ellipse will be of the form
The ellipse passes through points (4, 3) and (6, 2). Hence,
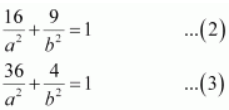
On solving equations (2) and (3), we obtain
a
2
= 52 and
b
2
= 13.
Thus, the equation of the ellipse is
.
.
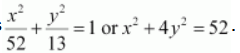