DIVISION OF POLYNOMIALS

The quotient law of exponents i.e. 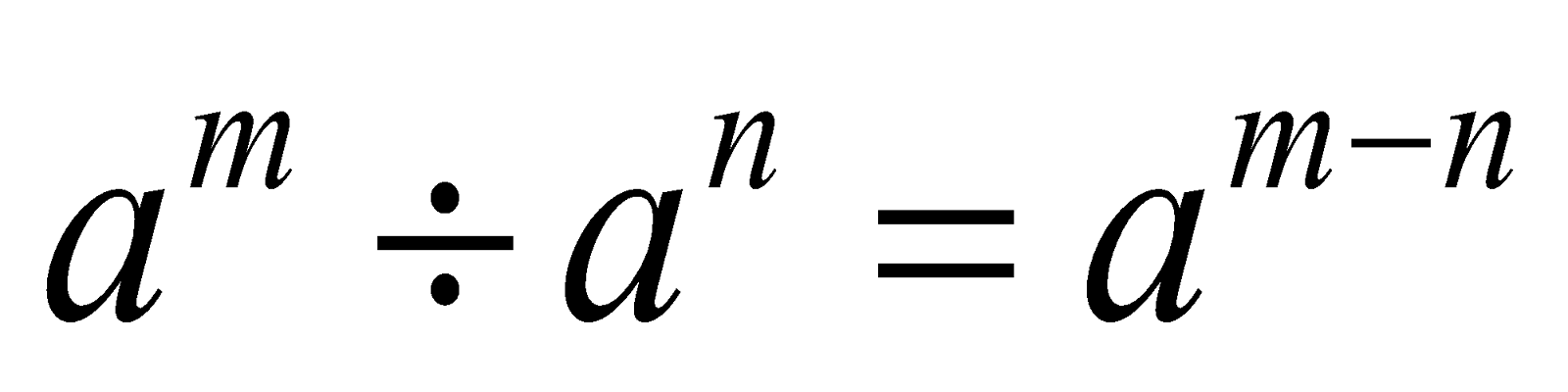finds great use in the division of algebraic expressions.

DIVISION OF A MONOMIAL BY A MONOMIAL:

Quotient of two monomials = (Quotient of their numerical coefficients) (Quotient of their variable parts)

Divide:

Q1. 24a2bc3 by – 6abc2 (ii) – 56 xyz3 by – 6x3y4z

Sol. (i) 24a2bc3 ÷  (-6abc2) =

.

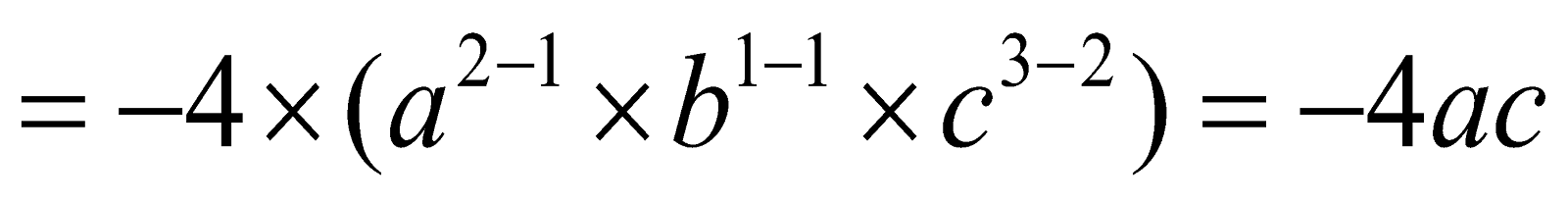(ii) (-56 xyz3) ÷ (-6x3y4z) =

.

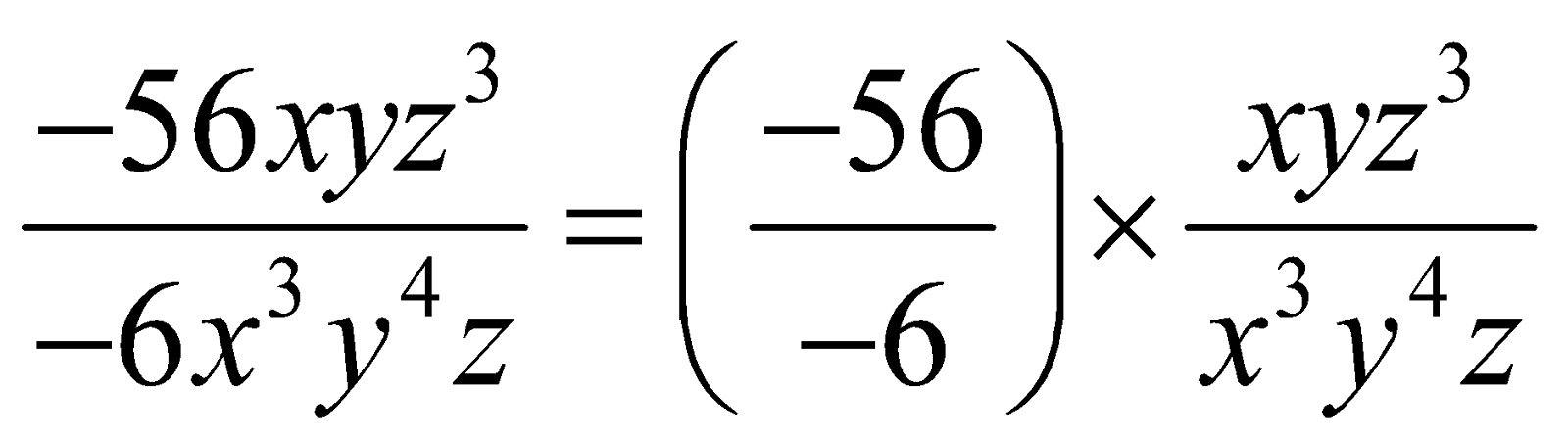
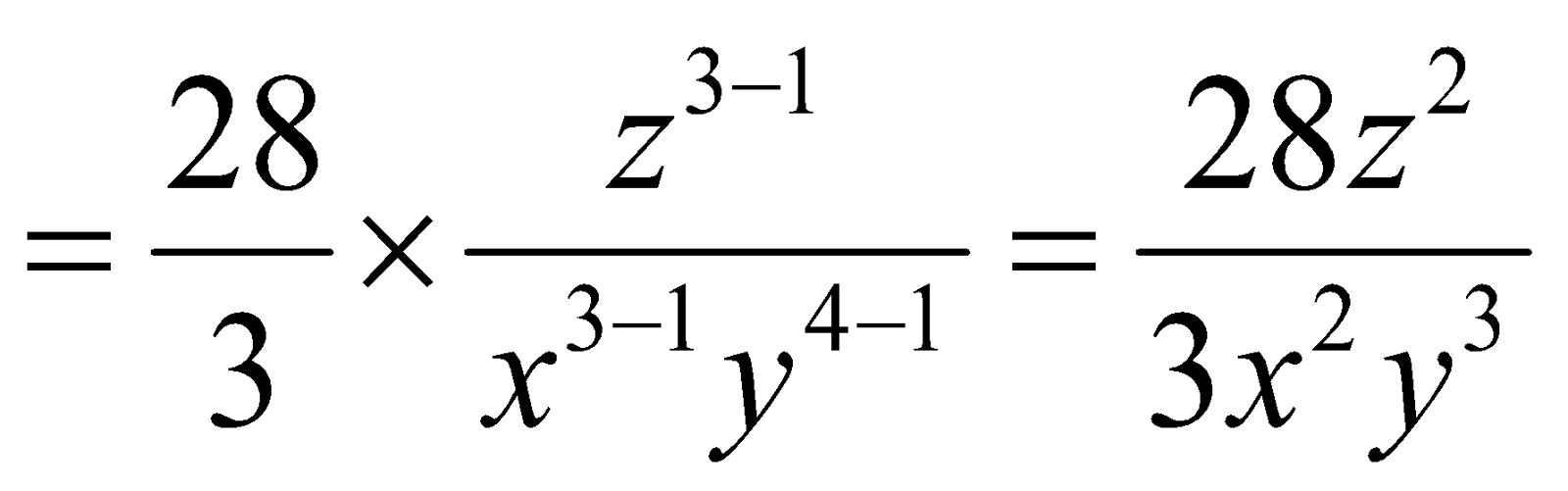DIVISION OF A POLYNOMIAL BY A MONOMIAL:

For dividing a polynomial by a monomial, we divide each term of the polynomial be the monomial.

Question (i)  4x5 – 14x4 + 6x3 – 2x2 by 2x2 (ii) 20x3y + 10xy2 – 15x2y by 5xy

Sol. We have :

(i) (4x5 – 14x4 + 6x3 – 2x2)  ÷  5x2

= .

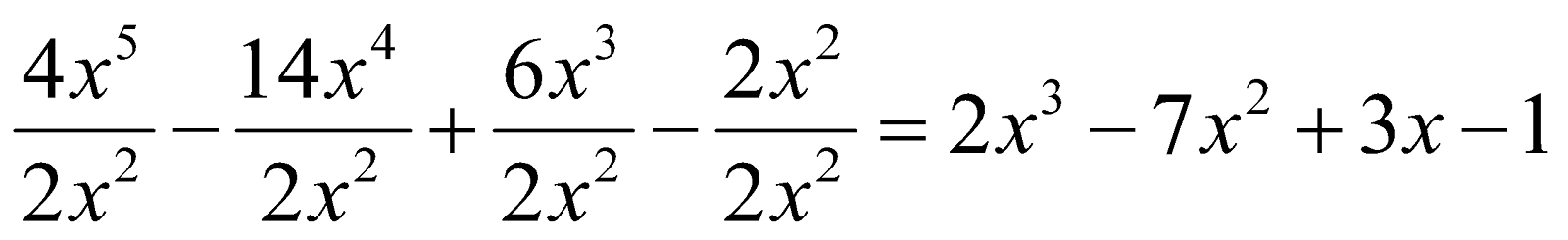(ii) (20x3y + 10xy2 – 15x2y) ÷ 5xy

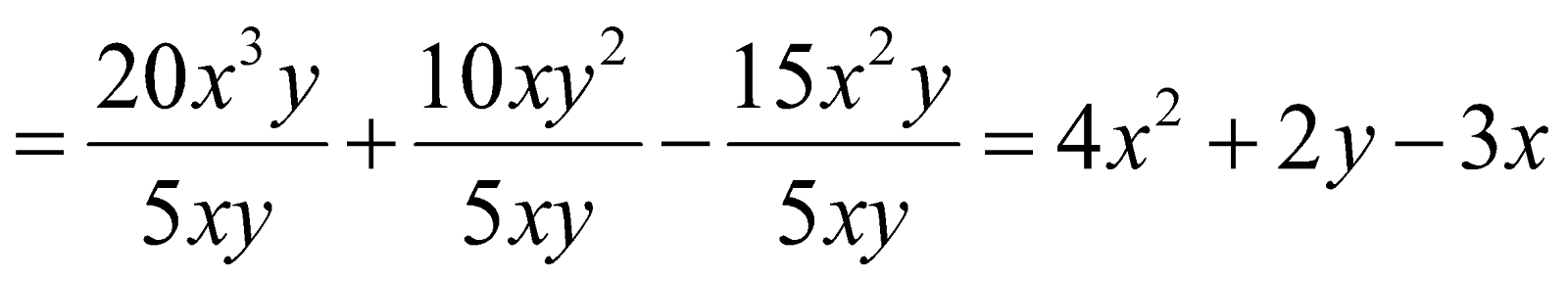
DIVISION OF A POLYNOMIAL BY A POLYNOMIAL:

Working Rule

Fundamentals propositions

• a  b × b = a
• a  b c = a  bc
• a  b × c = a × c  b

Sign convertions 

If a  b = c, then 

• (+ a)  (+ b) = + c
• (– a)  (– b) = + c
• ( – a)  (b) = – c
• (+ a)  (– b) = – c

Division of a monomial by a monomial

Quotient can be found by subtracting smaller power of a letter from greater power of the same letter.

E.g.: 16a5b4  8a2b3

To divide a multinomial by a monomial we have to divide each term of the dividend and take the sum of those partial quotients for the complete quotient

Ex: Divide 18x8 + 24x6 + 12x4  6x2

= 3x6 + 4x4 + 2x2

Division of a multinomial by another multinomial

• The dividend and the divisor both stand arranged according to descending powers of a common letter, namely, a 
• Divide the first term of the dividend by the first term of the divisor and write down the result as the first term of the quotient. Multiply the divisor by the quantity thus found and subtract the product from the dividend.
• (Regard the remainder as a new dividend and see if it is arranged according to the descending powers of the common letter. Divide its first terms by the first term of the divisor and write down the result as the next term of the quotient. Multiply the divisor by this term and subtract the product from the new dividend. Then goes similarly with the successive remainders until there is no remainder.

e.g.: x4 – 4x2 + 12x – 9  x2 – 2x + 3

Divided = x4 – 4x2 + 12x – 9

Divisor = x2 – 2x + 3

Quotient = x2 + 2x – 3

Remainder = 0

You will observe that

Dividend = Divisor × Quotient + Remainder

FOLLOW THESE STEPS

Solved Examples

Q1. Divide x + 6x2 – 15 by 2x – 3.

Ans. Arranging the terms of the dividend and the divisor in descending order of powers of x and then dividing, we get:

2x – 3   6x2 + x – 15    3x + 5

6x2 – 9x

10x – 15

10x – 15 

0

(6x2 + x - 15) ÷ (2x – 3) = (3x + 5).

Q2. Find the quotient and remainder when (x5 + 3x4 – 5x3 + 14x2 + 36x - 13) is divided by (x2 + 4x – 2).

Ans. On dividing, we get :

x2 + 4x – 2     x5 + 3x4 – 5x3 + 14x2 + 36 x – 13    x3 – x2 + x + 8

x5 + 4x4 – 2x3

-x4 – 3x + 14x2 + 36x - 13

-x4 – 4x3 + 2x2

x3 + 12x2 + 36x – 13

x3 + 4x2 – 2x 

8x2 + 38x – 13 

8x2 + 32x – 16

6x + 3

Quotient = x3 – x2 + x + 8, Remainder = 6x + 3.

IDENTITY:

An identity is an equality which is true for all values of the variable(s).

Standard identities

• Identity 1 : (a + b)2 = a2 + 2ab + b2
• Identity 2 : (a – b)2 = a2 – 2ab + b2
• Identity 3 : (a + b) (a – b) = a2 – b2
• Identity 4 : (x + a) (x + b) = x2 + (a + b) x + ab
• Identity 5 : (a + b + c)2 = (a2 + b2 + c2) + 2(ab + bc + ca)
• Identity 6 : (a + b – c)2 = (a2 + b2 + c2) + 2(ab – bc - ca)
• Identity 7 : (a + b)3 = a3 + b3 + 3ab (a + b)
• Identity 8 : (a - b)3 = a3 – b3 – 3ab (a – b)

General expressed in symbols is called a formula. Some of the formulae are listed below.

• (a + b)2 = a2 + 2ab + b2
• (a – b)2 = a2 – 2ab + b2
• (a – b)2 = (a + b)2 – 4ab
• (a + b)2 = (a – b)2 + 4ab
• (a + b)2 – (a – b)2 = 4ab
• (a + b)2 + (a – b)2 = 2(a2 + b2)
• a4 + a2b2 + b4 = (a2 + ab + b2) (a2 – ab + b2)
• (a + b)3 = a3 + b3 + 3ab (a + b) or a3 + b3 + 3a2b + 3ab2
• (a – b)3 = a3 – b3 – 3ab (a – b) or a3 – b3 – 3a2b + 3ab2
•  (a + b)3 + (a – b)3 = 2a3 + 6ab2
•  (a + b)3 – (a – b)3 = 2b3 + 6a2b
•  (a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
•  a3 + b3 + c3 – 3abc = (a + b + c) (a2 + b2 + c2 – ab – bc – ca)
•  If a + b + c = 0 then a3 + b3 + c3 = 3abc
•  a3 + b3 = (a + b) (a2 – ab + b2)
•  a3 – b3 = (a – b) (a2 + ab + b2)
•  (x + a) (x + b) (x + c) = x3 + x2 (a + b + c) + x (ab + bc + ca) + abc
• (x + a) (x + b) = x2 + x(a + b) + ab

Also Check

1. Type of Algebraic Expressions
2. Questions on Algebraic Expressions