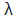Derivation Of Angular Momentum From De Broglie Equation
Atomic Structure of Class 11
According to Bohr’s model , the electron revolves around the nucleus in circular orbits. According to de Broglie concept, the electron is not only a particle but has a wave character also.
|
If the wave is completely in phase, the circumference of the orbit must be equal to an integral multiple of wave length (λ) Therefore 2πr = nλ where ‘n’ is an integer and ‘r’ is the radius of the orbit But λ = h/mv ∴ 2πr = nh /mv (or) mvr = n h/2π |
|
which is Bohr’s postulate of angular momentum, where ‘n’ is the principal
quantum number.
“Thus, the number of waves an electron makes in a particular Bohr orbit in one complete revolution is equal to the principal quantum number of the orbit”.
Alternatively Number of waves ‘n’=
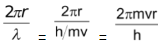
where v and r are the velocity of electron and radius of that particular Bohr orbit in which number of waves are to be calculated, respectively.
The electron is revolving around the nucleus in a circular orbit. How many revolutions it can make in one second
Let the velocity of electron be v m/sec. The distance it has to travel for one revolution 2πr, (i.e., the circumference of the circle).
Thus, the number of revolutions per second is = V/2πr
Common unit of energy is electron volt which is amount of energy given when an electron is accelerated by a potential of exactly 1 volt. This energy equals the product of voltage and charge. Since in SI units coulombs × volts = Joules, 1 eV numerically equals the electronic charge except that joule replaces coulombs.
Illustration 7:Two particles A and B are in motion. If the wavelength associated with
[Distinction between the wave- particle nature of a photon and the particle- wave nature of a sub atomic particle]
|
Photon |
Sub Atomic Particle |
|
1. Energy = hν |
Energy =
|
|
2. Wavelength =
|
Wavelength = h/mv |
[Note: We should never interchange any of the above]

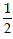 mv
2
mv
2