Molecular Orbital Theory

MOLECULAR ORBITAL THEORY

In Molecular Orbital Theory (MOT) the atoms in a molecule are supposed to loose their individual control over the electrons. The nuclei of the bonded atoms are considered to be present at equilibrium inter-nuclear positions. The orbitals where the probability of finding the electrons is maximum are multicentred orbitals called molecular orbitals extending over two or more nuclei.

In MOT the atomic orbitals loose their identity and the total number of electrons present are placed in MO’s according to increasing energy sequence (Aufbau Principle) with due reference to Pauli’s Exclusion Principle and Hund’s Rule of Maximum Multiplicity.

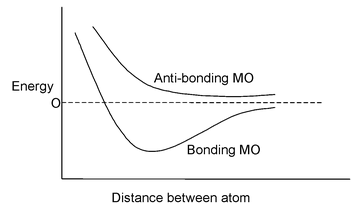
When a pair of atomic orbitals combine they give rise to a pair of molecular orbitals, the bonding and the anti-bonding. The number of molecular orbitals produced must always be equal to the number of atomic orbitals involved. Electron density is increased for the bonding MO’s in the inter-nuclear region but decreased for the anti-bonding MO’s, Shielding of the nuclei by increased electron density in bonding MO’s reduces inter nuclei repulsion and thus stabilizes the molecule whereas lower electron density even as compared to the individual atom in anti-bonding MO’s increases the repulsion and destabilizes the system.

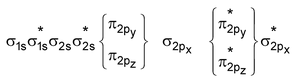
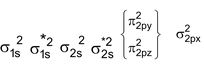
In denotion of MO’s, σ indicates head on overlap and  π represents side ways overlap of orbitals. In simple homonuclear diatomic molecules the order of MO’s  ( for molecules having total number of electrons less than 16) based on increasing energy is

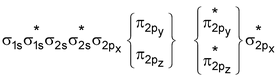
For molecules having total number of electrons equal to or more than 16 (including O₂ and above) the order is

If the molecule contains unpaired electrons in MO’s it will be paramagnetic but if all the electrons are paired up then the molecule will be diamagnetic. Paramagnetic substances are attracted in magnetic field whereas diamagnetic substances are repelled in magnetic field.

Bond order =

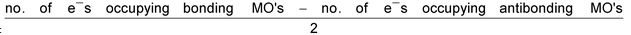
Application of MOT to homonuclear diatomic molecules.

H₂ Molecule : Total no. of electrons = 2

Arrangement :

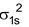
Bond order : ½ (2 – 0) = 1

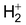Molecule : Total no. of electrons = 1

Arrangement :

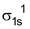
Bond order : ½ (1 – 0) = 1/2

He₂ Molecule : Total no. of electrons = 4

Arrangement :

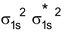
Bond order : ½ (2 – 2) = 0

∴He₂ molecule does not exist.

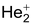Molecule : Total no. of electrons = 3

Arrangement :

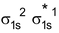
Bond order : ½ (2 – 1) = 1/2

So 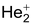exists and has been detected in discharge tubes.

Li₂ Molecule : Total no. of electrons = 6

Arrangement :

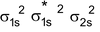
Bond order : ½ (4 – 2) = 1

No unpaired e’s so diamagnetic

Be₂ Molecule : Total no. of electrons = 8

Arrangement :   

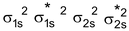
Bond order : ½ (4 – 4) = 0

No unpaired e–s so diamagnetic

B₂ Molecule : Total no. of electrons = 10

Arrangement :

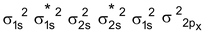
Bond order : ½ (6 – 4) = 1 ∴diamagnetic

But observed Boron is paramagnetic

C₂ Molecule : Total no. of electrons = 12

Arrangement :

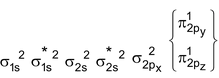
Bond order : ½ (4 – 0) = 2

It is paramagnetic

But observed C₂ is diamagnetic 

N₂ Molecule : Total no. of electrons = 14

Arrangement :

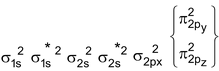
Bond order : ½ (6 – 0) = 3

∴ It is diamagnetic 

O₂ Molecule : Total no. of electrons = 16

Arrangement :

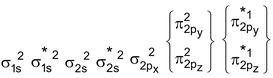
Bond order : ½ (6 – 2) = 2

It is paramagnetic

F₂ Molecule : Total no. of electrons = 18

Arrangement :

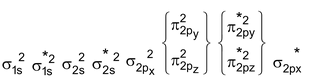
Bond order : ½ (6 – 4) = 1

B₂ :

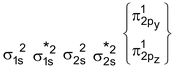
It is paramagnetic

C₂ :

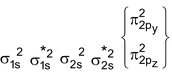
It is diamagnetic

N₂ :

It is diamagnetic