MOMENTUM

It is the combined effect of mass and velocity of the body. Mathematically, momentum of the body is defined as the product of mass and the velocity of the body. If m is the mass of the body and v is its velocity then momentum, p = mv

Momentum is a vector quantity and its direction is in the direction of velocity.

UNIT OF MOMENTUM:

(In C.G.S. system) 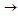p = mv 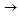gram × cm/s = dyne × s

(In M.K.S. system) 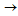p = mv 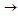kg ×  m/s = Newton × s

NEWTON’S SECOND LAW OF MOTION

According to this law, the rate of change of momentum of an object is proportional to the applied unbalanced force in the direction of force.

Now, Rate of change of momentum

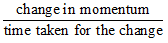
So, according to this law,

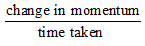∝ force applied

Mathematical formulation of Newton’s second law of motion:

Suppose of an object

m = mass

u = initial velocity along a straight line

F = constant external force

t = time for which the force is applied

v = final velocity along the same straight line after time, t.

Initial momentum of the object, p1 = mu

Final momentum of the object, p2 = mv

Change in the momentum = p2 – p1

= mv – mu

= m (v – u)

Rate of change of momentum

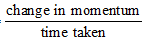
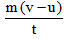= …(i)

But we know

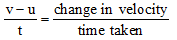
= rate of change of velocity

= acceleration of the object (a)

i.e. 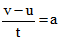…(ii)

Putting 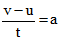from equation (ii) into (i)

We get,

Rate of change of momentum = m × a

According to Newton’s second law of motion rate of change of linear momentum ∝ Force applied

∴ m × a ∝ F

or F ∝ m a

or F = k m a

where k is a constant of proportionality. The value of constant k in S.I. units is 1, so the above equation becomes :

F = m × a

or Force = mass × acceleration

The S.I. unit of force is Newton which is denoted by N. A Newton is that force which when acting on a body of mass 1 kg produces an acceleration of 1 m/s 2 in it.

We know, F = m × a

IN = 1 kg × 1 m/s 2

The second law of motion gives us a method to measure the force acting on an object as a product of its mass and acceleration. While calculating, if a minus sign comes with the force, it will indicate that the force is acting in a direction opposite to that in which body is moving. Since force is a vector quantity.

Applications of Newton’s second law of motion:

Some of our day-to-day observations can be explained in terms of Newton’s second law of motion.

As

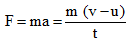
∴ The force F can be reduced by increasing the time taken t for the change in momentum of the body. For example :

(i) Catching a cricket ball: To catch a fast cricket ball, a player pulls his hands backwards to prevent injury to his hands. By doing so, the player increases the time during which high velocity of the cricket ball reduces to zero. Thus, the acceleration of the ball 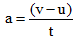is decreased, and therefore, the impact of catching the fast ball (i.e., F = ma) is reduced, i.e., the player has to apply a smaller force against the ball in order to stop it. The ball, in turn, exerts a smaller force on his hands and the hands are not injured.

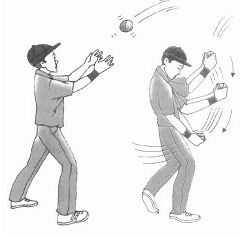
If the ball was stopped suddenly, the high velocity of the ball would be reduced to zero in a very short interval of time, t. Therefore, rate of change of linear momentum of the ball would be large, and therefore, a large force would have to be applied for holding the catch. The hands of the player would be hurt.

(ii) High Jump: In the athletic event ‘High Jump’, the athletes are made to fall either on a cushioned bed or on a sand bed. This is done to avoid injury to the athlete. Falling on a cushioned bed or on a sand bed will increase the time during which high velocity of the athlete would be reduced to zero. This would decrease the rate of change of momentum of the athlete and hence the force on the athlete. The injury to the athlete is thus avoided.

(iii) Use of seat belts in cars: All the cars these days are provided with seat belts for the passengers, which are rightly called safety belts. The purpose of seat belts is to prevent injuries to the passengers in case of an accident or in case of sudden application of brakes. In both the cases, the momentum of the car reduces to zero in a very short interval of time resulting in the development of a large force causing injuries. The stretchable safety belts worn by the passengers of the car exert a force on their body and make the forward motion slower. Thus, the time taken by the passengers to fall forward increases. Therefore, rate of change of momentum of passengers is reduced. Hence, the stopping force acting on the passengers is reduced. They may not get injuries at all or they may get away with minor injuries.