Newton's Law Of Gravitation
Gravitation of Class 11
The force of interaction between any two particles having masses m1 and m2 separated by a distance r is attractive and acts along the line joining the particles. The magnitude of the force is given by
F =
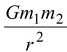 (11.1)
(11.1)
where G is a universal constant having the same value for all pairs of particles. Its numerical value is 6.67 × 10 -11 Nm2/kg2.
|
The gravitational forces between two particles are an action – reaction pair. The first particle exerts a force on the second particle that is directed towards the first particle along the line joining the two. |
|
- Similarly , the second particle exerts a force on the first particle that is directed towards the second particle along the line joining the two. These forces are equal in magnitude but oppositely directed.
- In the vector form, equation (11.1) may be written as
-
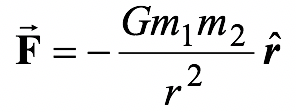 (11.2)
(11.2)
-
where one must remember that
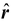 has its origin at the source of the force.
has its origin at the source of the force.
|
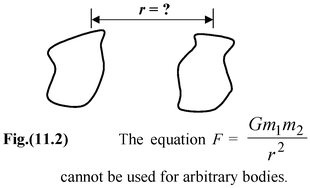
It is important to realize that Newton’s law of gravitation is stated only for point particles. For two arbitrary bodies, as shown in figure (11.2), there is no unique value for the separation r. |
|
To compute the force between them requires integral calculus. However, for the special case of a uniform spherical mass distribution, r may be taken as the distance to the center. Also, when the separation between two objects is very much larger than their sizes, they may be approximated as point masses and then, equation (11.1) may be used.
|
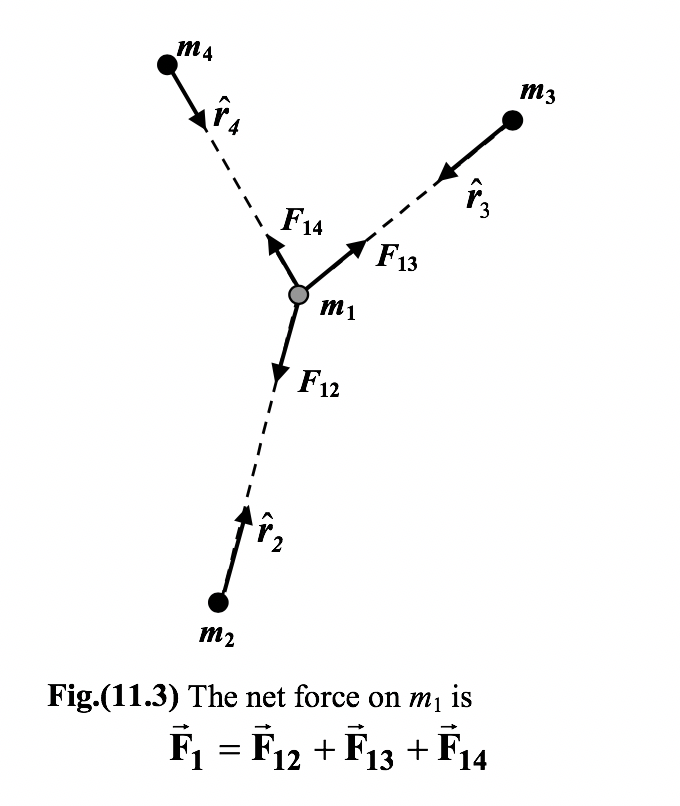
Principle of Superposition Experiments show that when several particles interact, the force between a given pair is independent of the other particles present. The net force F 1 on the point mass m1 due to the other particles as shown in the figure (11.3) is found by first calculating its interaction with each of the other particles one at a time. The net force on m1 is the vector sum of the pair-wise interactions. |
|
![]() (11.3)
(11.3)
Problem Solving Strategy:
- 1.Set up a convenient coordinate system
- Indicate the directions of the forces acting on the particle under consideration.
- Calculate the (scalar) magnitudes of the forces.
- Find the net force by using the component method.
|
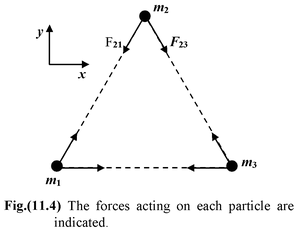
Example 11.1 Three point particles with masses m 1 = 4 kg, m 2 = 2 kg and m 3 = 3 kg are at the corners of an equilateral triangle of side L = 2m, as shown in figure. Find the net force on m 2 . |
|
Solution
- The first two steps have already been done in the figure. The magnitudes of forces are
- F 21 = Gm2m1/L2 = 1.33 × 10 -10 N
- F 23 = Gm2m3/L2 = 1.01 × 10 -10 N
- The net force on m 2 is
-
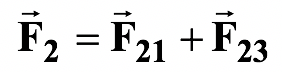
- Its components are
- F 2x = -F 21 cos60 o + F 23 cos60 o = -1.6 × 10 -11 N
- F 2y = -F21sin60 o – F 23 sin60 o = -2.03 × 10 -10 N
- Thus,
F
2
= -(1.6
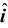 + 20.3
+ 20.3
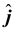 ) × 10
-11
N
) × 10
-11
N