Motion In Two Dimensions
Kinematics of Class 11
Motion In Two Dimensions
|
Whatever we have studied in the kinematics of one dimensional motion the same is applicable for motion in two and three dimensions. In two dimensions the position vector r of a particle whose coordinate are (x, y) is
r = x
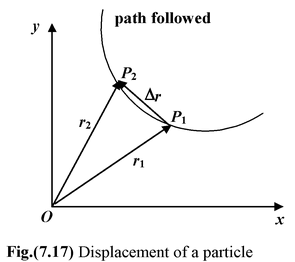
If the particle moves from P1 at position r1 to P2 at position r2, as shown in figure its displacement is given by
Δr = r
2
− r
1
= Δx
|
|
|
The student must carefully note the correct direction of Δr. Δr is the vector that must be added to the initial position r1 to give the final position r 2 , i.e. r 2 = r 1 + Δr The average velocity is defined as the ratio of the displacement over the time interval vav = Δr/Δt |
|
or v = dr/dt = vx
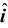 + vy
+ vy
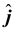 (7.13)
(7.13)
where vx = dx/dt and v y = dy/dt
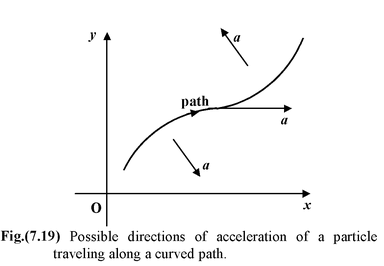
The direction of v is along the tangent to the path.
|
The instantaneous acceleration is the ratio of change of the velocity with respect to time.
a =
where a x =
Note that one cannot determine acceleration directly from the path of the particle. One needs to know how each component of the velocity varies as function of space and time. |
|
General equations of kinematics for constant acceleration
v = v 0 + at(7.15)
r = r 0 + v 0 t + 1/2 at 2 (7.16)
r = r 0 + 1/2 (v 0 + v)t(7.17)
For two−dimensional motion in the plane, the x and y components of these equations are:
vx = v 0 x + axtvy = v 0 y + ayt
x = x 0 + v 0 x + 1/2 axt2y = y 0 + y 0 yt + 1/2 ayt 2
x = x 0 + 1/2 (v 0 x + vx)ty = y 0 + 1/2(v 0 y + vy)t
Example : 7.11
|
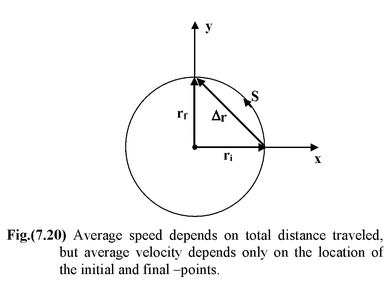
A particle moves one quarter of a circular path of radius 20 m in 10 s. Its initial position is given by ri = (20 m)i and its final position is rf = (20m)j . (a)Find its displacement Δr and average velocity vav (b)Find the magnitude of its average velocity and its average speed. Solution (a)The displacement is given by
or
and the average velocity is |
|
![]() (m/s)
(m/s)
(b)The magnitude of the average velocity is
![]() m/s
m/s
Average speed =
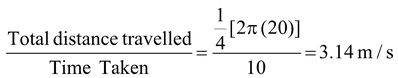


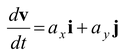 (7.14)
(7.14)