Projectile Motion
Kinematics of Class 11
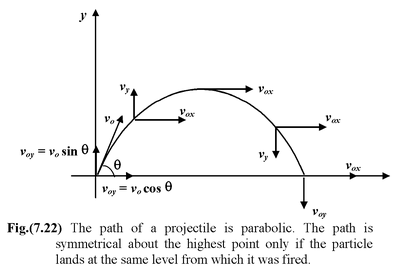
A projectile motion near the surface of the earth consists of two independent motions, a horizontal motion at constant speed and a vertical one subject to the acceleration due to gravity.
In order to deal with problems in projectile motion, one has to choose a coordinate system and clearly specify the origin. If the x axis is horizontal and the y−axis points vertically upward, then
ax= 0 and ay = −g
One can easily assume the origin such that the initial horizontal coordinate is zero.
i.e.xo= 0
The equations of kinematics for projectile motion are
x = v ox t(7.18)
vy= v o y−gt(7.19)
y = yo+ v o yt −1/2 gt 2 (7.20)
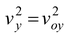 −2g (y−y
o
)(7.21)
−2g (y−y
o
)(7.21)
Example 7.12
A ball is projected horizontally at 20 m/s from a cliff of height 45 m
(a)Find its time of flight
(b)Find its horizontal range R (the horizontal displacement from the point of firing).
Solution
The origin is assumed to be at the base of the cliff
Given: x o =0; y o = 45 m; v ox = 20 m/s and v oy = 0
The coordinates at a latter time are given by
x = 20 t(i)
x = 45 − 5t2(ii)
(a)When the ball lands, its vertical coordinate is zero
i.e. y = 0 From (ii) , we get
0 = 45 − 5t 2 ort = 3 s
Note that the time of flight does not depend on the value of the horizontal component of the initial velocity. If the ball were dropped from the same height it would have reached the ground in 3 s.
(b)To find the horizontal range we use the horizontal velocity and the time of flight.
R = v ox t = (20) (3) = 60 m
Example 7.13
A ball is projected from the ground with an initial velocity voat an angle θ above the horizontal
(a)Find the time of flight
(b)Determine the horizontal range R
(c)Determine the maximum height obtained by the ball
(d)Obtain an expression for the trajectory of projectile
Solution
The origin is assumed at the point of projection. The instantaneous x and y coordinates of the ball are given by
x = (v 0 cos θ) t(i)
y = (v 0 sin θ) t−1/2 gt 2 (ii)
(a)To find the time of flight, we put y = 0 in equation (ii)
0 = (v 0 sin θ) t−1/2 gt 2
or t =
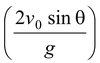 ..(iii)
..(iii)
(b)To find the horizontal range we substitute (iii) in (i)
R = (vo cos θ)
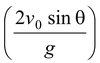
or R =
 (iv)
(iv)
|
(c)The maximum height H for the projectile is given by
Since vy=0, therefore,
H =
(d)To find the trajectory of the projectile we have to express y in terms of x. Therefore eliminating t from (i) and (ii), we get |
|
y = x tan θ−
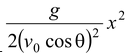 (vi)
(vi)
IMPORTANT1.The time of flight is given by
T =
2.The horizontal range is given by
R =
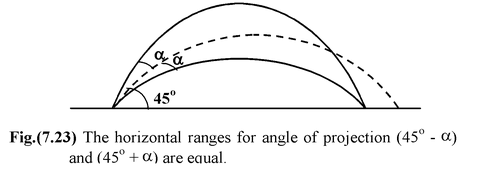
Equations (7.22) and (7.23) are valid only when the projectile returns to the initial vertical level. For a given initial speed vo, the range is a maximum when sin 2θ =1, that is when θ = 45°. For a given velocity vosame range occurs at two angles of projection, viz. θ = 45 ± α
|
|
3.The maximum height of the projectile is
H =
4.The trajectory of a projectile is a parabola
y = xtan θ−
|
Example: 7.14
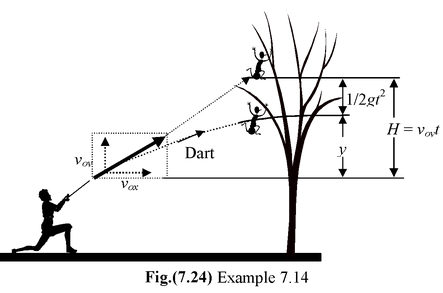
A hunter with a blowgun wishes to shoot a monkey hanging from a branch. The hunter aims right at the monkey, not realizing that the dart will follow a parabolic path and thus fall below the monkey. The monkey, however seeing the dart leave the gun, lets go of the branch and drops out of the tree, expecting to avoid the dart. Show that the monkey will be hit regardless of the initial velocity of the dart so long as it is great enough to travel the horizontal distance to the tree before hitting the ground.
Solution
Let the horizontal distance to the tree be x and the original height of the monkey be H, as shown in Fig. (7.24). Then the dart will be projected at an angle given by tan θ = H/x
If there were no gravity, the dart would reach the height H in the time t taken for it to travel horizontal distance x:
y = v
oy
t = Hin time t =
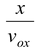 with no gravity
with no gravity
|
andy = v oy t −1/2gt2with gravity ory = H −1/2gt 2 This is lower than H by 1/2gt 2 , which is just the amount the monkey falls in this time. The initial velocity of the dart is varied so that for large v0the target is hit very near its original height and for small v0it is hit just before it reaches the floor. |
|

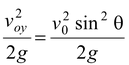 (v)
(v)
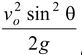 (7.24)
(7.24)