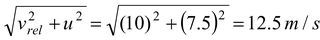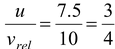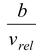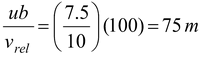Relative Velocity
Kinematics of Class 11
The motion of anybody has to be described relative to some frame of reference, such as the ground. Sometimes it becomes necessary to study the motion of one body relative to another body which is also moving relative to the ground. Let us study the relative motion in general.
|
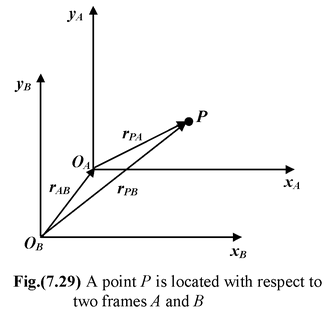
Consider the particle P which is being observed from two frames A and B. Its positions with respect to frames A and B are rPA and rPB, respectively.
The position vector triangle is shown in the rPB = rPA + rAB (7.27) Position of P Position of P Position of A w.r.t. B w.r.t. A w.r.t. B Differentiating the above equation, we get vPB= vPA+ vAB(7.28) |
|
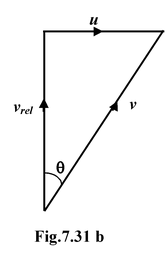
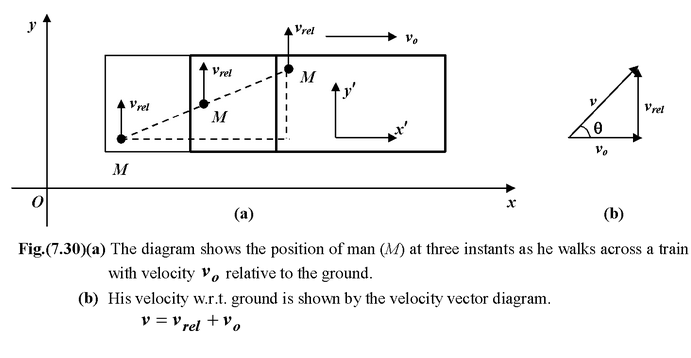
Note that equation (7.28) is a vector sum we worry about signs only when we take components. Let us consider the case where a man walks across a train with velocity vo. The ground forms a stationary frame (x, y) while the train forms a moving frame (x′, y′). We want to find the velocity of the man relative to the ground (v).
Using equation (7.28)
v = vrel+ v0
An observer on the train will see the man walking along the x′ axis. An observer on the ground will see him moving in a direction given by tan θ = 
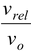to the x−axis.
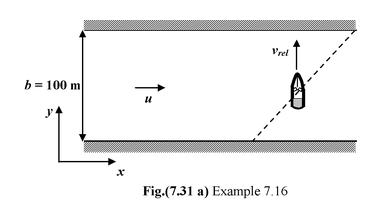
Example 7.16
A boat can travel at 10 m/s relative to the water. It starts at one bank of river that is 100 m wide and flows with a velocity u = 7.5 m/s. If the boat points directly across, find
(a)Its velocity relative to the bank
(b)How far downstream it travels.
|
Solution In this problem the train is replaced by the river and the man is replaced by the boat (a)From the velocity vector diagram, the magnitude of the velocity of boat w.r.t. ground is
v= The direction is indicated by the angle θ with the y−axis.
tan θ = |
|
|
or θ = tan−1(3/4) = 37° (b)The distance travelled along the bank is x = ut where t is the time taken to cross the river.
t = Thus,
x = |
|
Example 7.17
In which direction the boat must point so as to cross the river in a direction perpendicular to river currents. Also, find out the time taken to cross the river. Use the information given in the previous Example 7.16.
Solution
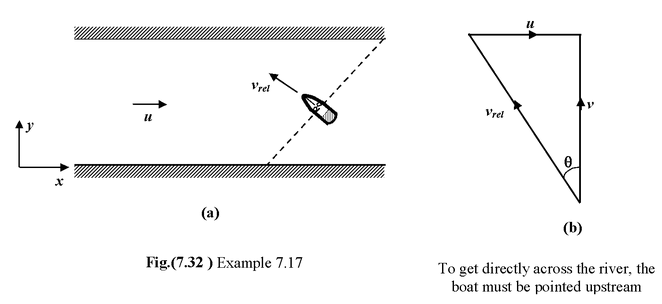
From the velocity diagram
The magnitude of the velocity w.r.t. bank is
v = 
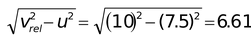m/s
The direction of motion of the boat w.r.t. the river current is represented by the angle θ measured anticlockwise from the y−axis.
tan θ = u/v = 7.5/6.61 - 1.13
or θ = tan−1 (1.13) = 48.6°
and time taken t = b/v = 100/6.61 = 15.13 s
