Angle Of Friction
Laws Of Motion of Class 11
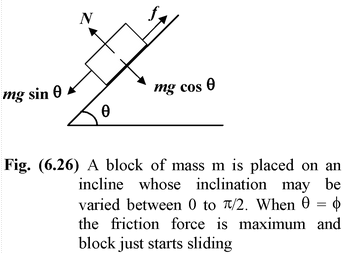
ANGLE OF FRICTIONSuppose a body is placed on an inclined surface whose angle of inclination θ varies between 0 to π/2. The coefficient of friction between the body and the surface is µs. Let the initial value of θ be zero and if we slowly start increasing the value of θ, then at a particular value of θ = φ the block just starts to move. This value of θ =φ is called the angle of friction. Mathematically, if the block is just about to move, thenmg sin θ = f Whenθ = φ, mg sin φ =fmax ormg sin φ = µsN = µsmg cos φ ortanφ = µs Thusφ = tan−1µs |
|
The angle of friction is that minimum angle of inclination of the inclined plane at which a body placed at rest on the inclined plane is about to slide down.
When θ ≤ φ (or tan1µs) the body is in equilibrium.
When the angle of inclination is more than the angle of friction (θ > φ) the block starts sliding down with acceleration. And, if we wish to keep it in equilibrium an external force has to be applied.
|
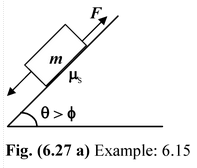
Example : 6.15 A block of mass m is placed at rest on an inclined plane whose angle with the horizontal is more than the angle of friction (θ > φ). An external force parallel to the inclined plane is applied in the upward direction to keep it in equilibrium. Find the magnitude of the force F. |
|
|
|
Solution
Since the block has a tendency to move downward, the force of friction acts upward on the block as shown in its free body diagram.
Applying equation of equilibrium, N = mg cos θ F + fmax = mg sin θ orF = mg sin θ − fmax = mg sin θ − µsmg cos θ orF = mg (sin θ − µs cos θ) |
|
|
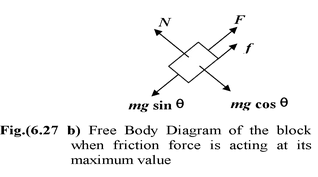
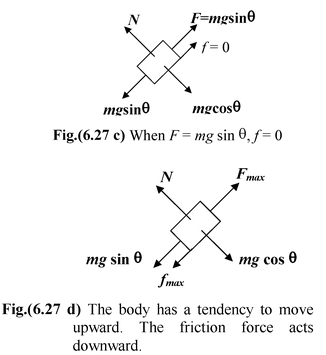
Note that this is the minimum magnitude of force required to keep it in equilibrium. If we apply a force slightly more than this the block does not start moving up but the magnitude of the friction force gets reduced. It becomes equal to zero when the external force attain a value equal to F = mg sin θ, as shown in Fig. (6.27c).
|
If the magnitude of F is further increased then the block has a tendency to move upward; the direction of friction force gets reversed. The block will not start moving up unless the external force attains the maximum value. The free body diagram of the body is shown in Fig. (6.27 d) Applying the equations of equilibrium N = mg cos θ Fmax = mg sin θ + fmax orFmax = mg (sin θ + µs cos θ) Conclusion The block remains stationary if Fmin ≤ F ≤ F max or mg(sin θ −µs cos θ) ≤ F ≤ mg(sin θ + µs cos θ) |
|
Example: 6.16
|
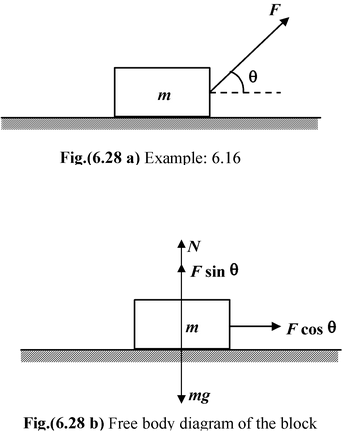
A block is placed at rest on a horizontal surface. The coefficient of friction between the block and the surface is µs. It is pulled with a force F at an angle θ with the horizontal as shown in the figure. Find the value of θ at which minimum force is required to move the block. Solution The free body diagram of the block is shown in the figure. Applying Newton’s Second Law N + F sin θ = mg(i) F cos θ = fmax = µsN(ii) orF cos θ = µs(mg − Fsin θ) orF(cos θ + µssin θ) = µsmg(iii) For minimum value of F, |
|
dF/dθ = 0
Thus, differentiating equation (iii) w.r.t. θ, by applying chain rule, we get
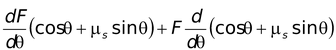 = 0
= 0
dF/dθ (cos θ + µssin θ) + F (−sin θ + µscos θ) = 0
Since dF/dθ =0, therefore (−sin θ + µscos θ )= 0
ortan θ = µs
⇒ θ = tan−1 µs
Note that minimum force is required to move the block at the angle of friction.
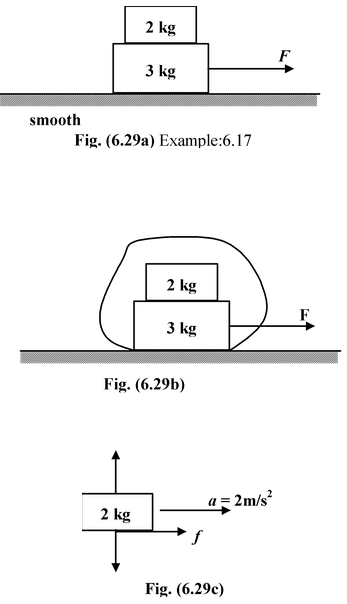
Example: 6.17
|
A small block of mass 2 kg is placed at rest on a large block of mass 3 kg. The coefficient of friction between the two blocks is µs = 0.3 and μk = 0.2. The horizontal surface is smooth. A horizontal force F is applied on the lower block. Find the acceleration of each block when (a) F = 10 N(b) F = 20 N Solution (a)Let us consider both the blocks move together. Then they by observing the free body diagram, we have
a =
Now, we have to check whether the two blocks really move together or not. For this we find the force of friction between the two blocks and if it is found to be less than or equal to fmax then the blocks move together. From the free body diagram of the 2 kg block f = ma =(2) (2) = 4 N Since fs(max) = µsN = (0.3) (20) = 6 N and f < fs(max) Thus, the blocks move together with an acceleration a = 2 m/s2 |
|
|
|
(b)Assuming the blocks move together
a =
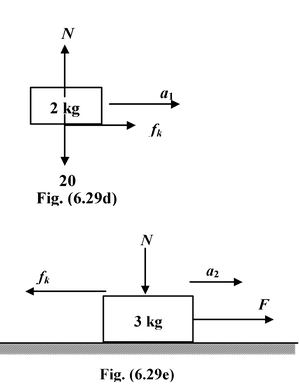
From the free body diagram of the 2 kg block, we get f = ma = (2) (4) = 8 N > fmax The blocks do not move together but moves relative to each other so kinetic friction starts acting. fk =μkN = 0.2(2)g = 4 N Applying Newton’s Second Law, Block m = 2kg;fk = 2a1
or a1 =
Block m = 3kg; F−fk = 3a 2 or a2 = 20 - 4/3 = 16/3 m/s 2 |
|
|

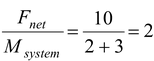 m/s
2
m/s
2
 m/s2
m/s2
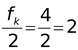 m/s
2
m/s
2