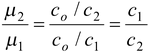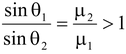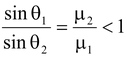Geometrical Optics

GEOMETRICAL OPTICS 

To a first approximation, we can consider the propagation of light disregarding its wave nature and assuming that light propagates in straight lines called rays. This allows us to formulate the laws of optics in the language of geometry. Thus, the branch of optics where the wave nature of light is neglected is called geometrical (or ray) optics. 

Geometrical optics is based on four laws:

1.Law of Rectilinear Propagation of Light.

It states that light propagates in straight lines in homogenous media. 

2.Law of Independence of Light Rays 

It states that rays do not disturb each other upon intersection. 

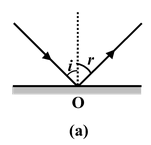
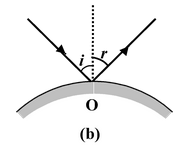
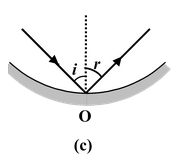
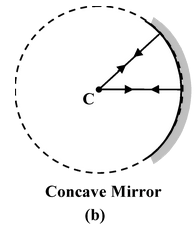
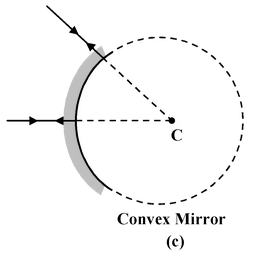
Laws of Reflection 

(i)The incident-ray, the reflected-ray and the normal to the reflecting surface at the point of incidence all lie in the same plane.

(ii)The angle of reflection (r) is equal to the angle of incidence(i)  i.e. i = r.

These laws are applicable to all reflecting surfaces either plane or curved. 

1.If i = 0 by i = r, r = 0 i.e., if a ray is incident normally on a boundary, after reflection it retraces its path.

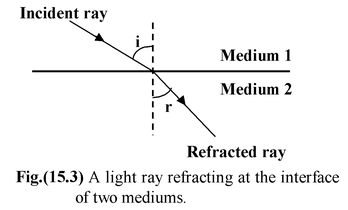
Laws of Refraction

(i)The incident ray, the refracted ray and the normal to the refracting surface at the point of incidence all lie in the same plane. 

(ii)The ratio of the sines of the angle of incidence (i) and that of the angle of refraction (r) is a constant quantity for two given media. 

The relative refractive index for two media is equal to the ratio of their absolute refractive indices. 

μ21 = μ2/μ1(15.1)

where μ2 and μ1 are the absolute refractive indices of the second and first media. 

The absolute refractive index of a medium is defined as the ratio of the speed of light in vacuum to the speed of light in the medium. 

μ = 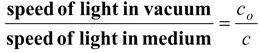(15.2)

Example 15.1

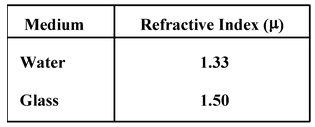
Refractive index of glass with respect to water is 1.125. Find the absolute refractive index of water, if the absolute refractive index of glass is 1.5.

Solution 

The refractive index of glass with respect to water is  μgw = μg/μw

orμw = μg/μgw = 1.5/1.125 = 1.33

Example 15.2 

The velocity of light in air is 3 × 108 m/s. Find the velocity of light in glass of refractive index 1.5. If the wavelength of yellow light in air is 6000Å, find its wavelength in the glass. 

Solution 

Let c1 and c2 be the velocities of light in air and glass respectively. 

Using the definition of refractive index. 

μ = c1/c2

orc2 = c1/μ

c2 = 3 x 10⁸/1.5 = 2 x 10⁸ m/s

Since frequency remains same when light passes from one medium to another. 

Therefore c1 = λ1f c2 = λ2f 

Now μ = c1/c2 = λ1/λ2

or λ2 =  λ1/μ =6000/1.5 = 4000Å

When light propagates through a series of layers of different medium as shown in the figure, then the Snell’s law may be written as 

μ1 sin θ1 = μ2 sin θ2 = μ3 sin θ3 = μ4 sin θ4 = constant 

In general,  μ sin θ = constant(15.4) 

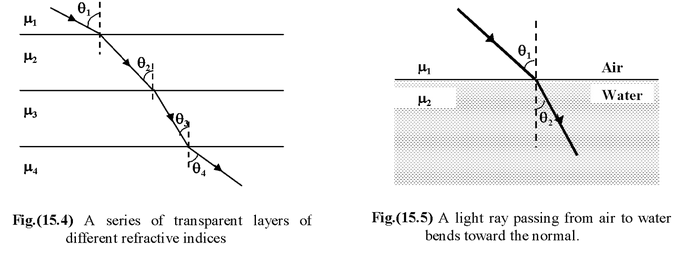
When light passes from rarer to denser medium it bends toward the normal as shown in the fig(15.5).

According to Snell’s law 

μ1 sin θ1 = μ2 sin θ2

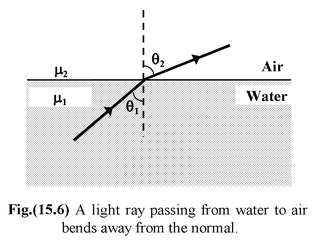
Thus, sin θ1 < sin θ2 ⇒θ1 < θ2

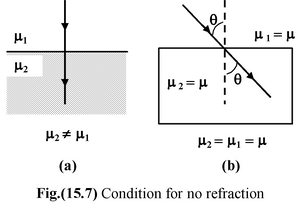
If light is incident normal to a boundary (i.e. i = 0), then, it passes undeviated from the boundary as shown in the fig.(15.7 a). 

Basic Problem in Optics

To find the position and nature of the final image formed by certain optical systems for a given object. The optical system may be just a mirror, or a lens or a combination of several reflecting and refracting surfaces. 

Basic Strategy 

First of all, we identify the sequence in which the reflection and refraction are taking place. The several events of reflection or refraction can be named as event 1, event 2 and so on following the sequence in which they occur. Now, the image of event 1 would be object for event 2, image of event 2 will be object of event 3 and so on. This way one can proceed to find the final image.