
REMAINDER THEOREM
Polynomial of Class 9
REMAINDER THEOREM
Let p(x) be any polynomial of degree greater than or equal to 1 and let a be any real number . If p(x) is divided by the linear polynomial x – a, then the remainder is p(a).
Proof :Let p(x) be any polynomial with degree greater than or equal to one. Suppose that when p(x) is divided by x-a, the quotient is q(x) and the remainder is r(x) , i.e.,
p(x) = (x-a)q(x) + r(x)…(i)
Since the degree of x - a is one and the degree of r(x) is less than the degree of x - a , it implies that the degree of r(x) = 0 This means that r(x) , is a constant, say r.
∴ So, for every value of x we have r(x) = r.
Therefore equation (i) becomes p(x) = (x - a) q(x) + r
In particular, if x = a above equation gives us
p(a) = (a - a) q(a) + r
0.q(a) + r
p(a) = r
which proves the theorem.
Question Find the remainder when f(x) = x 3 – 6x 2 + 2x – 4 is divided by g(x) = 1 – 2x.
Solution: Put g(x) = 1 – 2x = 0 ⇒ 2x = 1 ⇒ x = 1/2
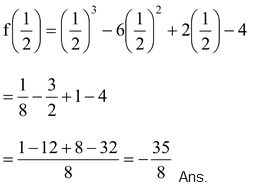
.
Question The polynomials ax 3 + 3x 2 – 13 and 2x 3 – 5x + a are divided by x + 2 if the remainder in each case is the same, find the value of a.
Solution: p(x) = ax 3 + 3x 2 – 13 and q(x) = 2x 3 – 5x + a
when p(x) & q(x) are divided by x + 2 = 0 ⇒ x = –2
p (–2) = q(–2)
⇒ a(–2) 3 + 3(–2) 3 – 13 = 2(–2) 3 – 5(–2) + a
⇒ –8a + 12 – 13 = –16 + 10 + a
⇒ –9a = –5
⇒ a = 5/9 Ans.
FACTOR THEOREM:
Statement: If p(x) is a polynomial of degree n ≥ 1 and a is any real number, then (i) x - a is a factor of p(x) , if p(a) = 0 , and (ii) p(a) = 0 if x- a is a factor of p(x).
Proof: By the Remainder Theorem we have, p(x) = (x - a) q(x) + p(a).
(i) If p(a)= 0 then p(x) = (x - a) q(x) which indicates that x - a is a factor of p(x)
(ii) Since x - a is a factor of p(x) ,p(x) = (x - a) g(x) for some polynomial g(x) . In this case, p(a) = ( a - a)g(a) = 0
Question Show that x + 1 an d 2x - 3 are factors of 2x 3 – 9x 2 + x + 12.
Solution: To prove that (x + 1) and (2x - 3) are factors of 2x 3 – 9x 2 + x + 12 it is sufficient to show that p(–1) and p(3/2) both are equal to zero.
p(–1) = 2(–1) 3 – 9(–1) 2 + (–1) + 12 = –2 – 9 – 1 + 12 = –12 + 12 = 0
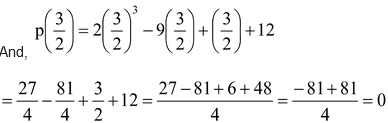
Hence, (x + 1) and (2x – 3) are the factors 2x 3 – 9x 2 + x + 12. Ans.
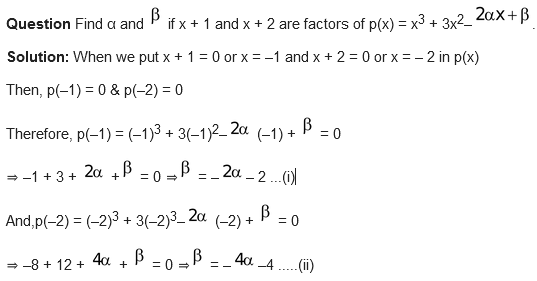
From equation (i) and (ii)
–2α– 2 = –4α– 4
⇒2α = – 2 ⇒α = –1
Put α= –1 in equation (i) ⇒β = –2(–1) – 2 = 2 – 2 = 0.
Hence,α= –1 β= 0. Ans.
Division of polynomials
Long division method
Long division for polynomials works in much the same way:
Question
Divide
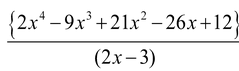 by long division method
by long division method
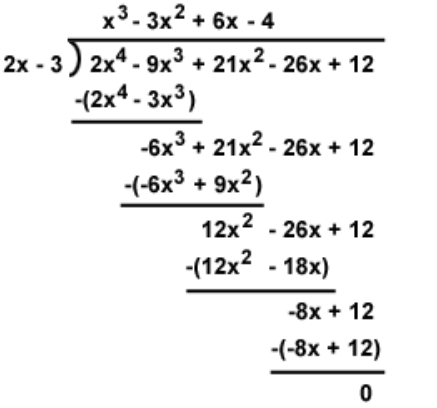
Question
Divide
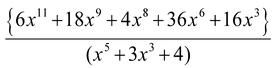 by long division method
by long division method
Solution:

Other Resourceful Topics






