Moment Of Inertia
Rotational Motion of Class 11
The moment of inertia (I) of a body is a measure of its rotational inertia, that is, its resistance to change in its angular velocity. It depends on the location of the axis, that is, on how the mass of the body is distributed relative to the axis. Thus, a body does not posses a unique moment of inertia; different axes through the body are associated with different moments of inertia.
|
For a discrete system of particles the moment of inertia is defined as I = Σm i r i 2 (10.15) wheremi is the mass of the ith particle andri is the perpendicular distance of the ith particle from the axis of rotation. |
|
|
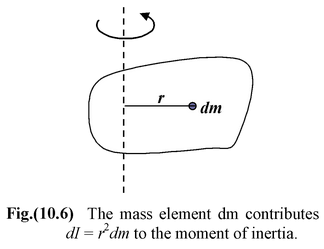
For a continuous system, the mass element should be chosen such that all the particles on it are at the same perpendicular distance from the axis. The moment of inertia of the whole body is given by I = ∫ r 2 dm (10.16) where r is the perpendicular distance of the element dm from the axis. |
|
|
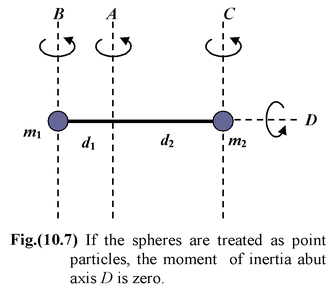
Example 10.4 Many molecules have a simple diatomic, dumbbell structure. Let us find the moments of inertia about four axes. We treat the bodies as point particles with mass m 1 = 3 kg and m2 = 5 kg. Take d 1 = 1m and d 2 = 2 m in figure (10.7). |
|
Solution
Axis A: IA = m 1 d 1 2 + m 2 d 2 2 = (3 kg)(1 m) 2 + (5 kg)(2m) 2 = 23 kgm 2
Axis B:IB = m 1 (0) + m 2 (d 1 + d 2 ) 2 = 45 kg m 2
Axis C:IC = m 1 (d 1 + d 2 ) 2 + m 2 (0) = 27 kg m 2
Axis D:ID = 0
ID is zero because we treated the masses as point particles and perpendicular distances are equal to zero.
Example 10.5
|
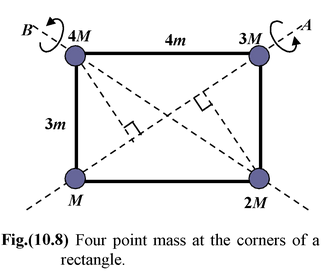
Four point masses lie at the corners of a rectangle with sides of length 3 m and 4m, as shown in figure. Find the moment of inertia about each of the diagonals. Take
|
|
Solution
For each mass we need its perpendicular distance from the axis. For each axis, two masses do not contribute to the moment of inertia. The other two are at the same distance
3 sin53 o = 2.4 m.
IA = (4 kg)(2.4 m) 2 + (2 kg)(2.4 m) 2 = 34.6 kg m 2
IB = (1 kg)(2.4 m) 2 + (3 kg)(2.4 m 2 ) = 23. 0 kg m 2
Example 10.6
|
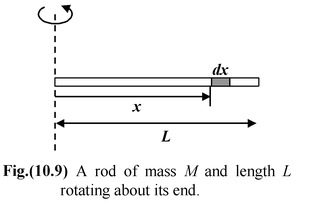
Find the moment of inertia of a thin rod of mass M and length L about an axis at one end and perpendicular to the rod, as shown in the figure. |
|
Solution
The mass of an element of length dx is dm = λ dx,
where λ = M/L is the linear mass density.
The moment of inertia of the mass element that is at a distance x from the axis is
dI = x 2 (λdx). For the entire rod the moment of inertia is
I =
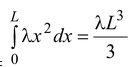
Since M = λL,
Iend =
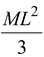
The Parallel Axis Theorem
Let the moment of inertia of an object through its center of mass be Icm. The moment of inertia of the mass through any other axis parallel to the first is given by
Iparallel = Icm + Mh 2 (10.17)
where M is the total mass of the object and h is the perpendicular distance between the two parallel axes.
|
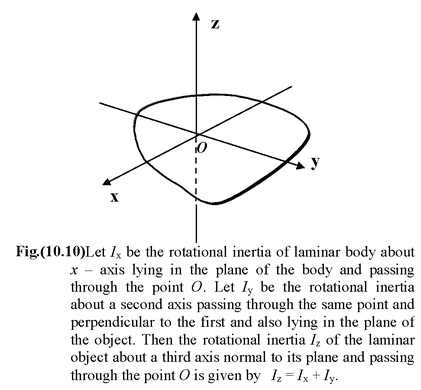
Perpendicular Axis Theorem By a laminar body we mean an object that can be treated as two – dimensional, such as a large figure cut from a thin sheet of plywood. Let the z axis be perpendicular to a laminar body and run through any point O in the plane of the body. Let the moment of inertia of the body about that axis be Iz. Let the x and y be two mutually perpendicular axes lying in the plane of the body with the origin at the point O as shown in figure. Let the moment of inertia about the x and y axes to be Ix and Iy. The perpendicular axis theorem states that Iz = Ix + Iy (10.18) |
|
Example 10.7
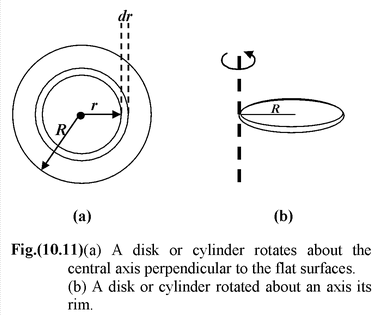
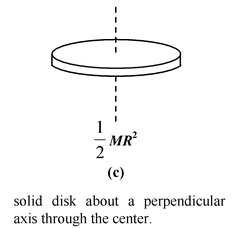
Find the moment of inertia of a circular disc or solid cylinder of radius R about the following axes.
(a)through the center and perpendicular to the flat surface.
(b)at the rim and perpendicular to the flat surface
|
Solution
(a)Figure (10.11 a) shows that the appropriate mass element is a circular ring of radius r and width dr. Its area is dA = 2πrdr and its mass is
dI = r 2 dm = 2πσr 3 dr For the whole body,
I = 2πσ
The mass of the whole disk or cylinder is M = σA = σπR2, and so
Icm =
|
|
(b)The evaluation of the moment of inertia about an axis at the rim, as in figure, by integration is difficult. The parallel axis theorem, equation, with h = R, provides the answer with remarkable simplicity.
Irim = Icm + Mh
2
=
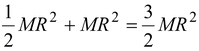
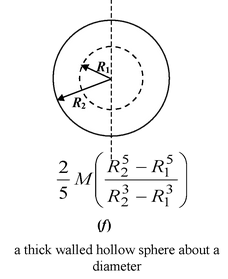
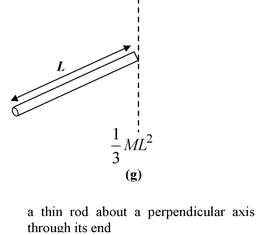
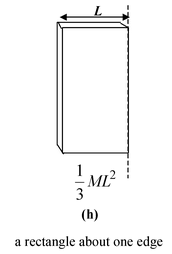
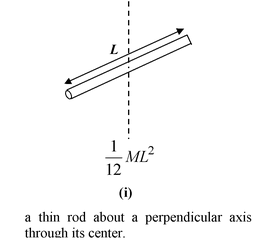
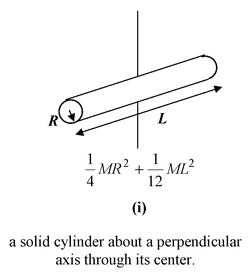
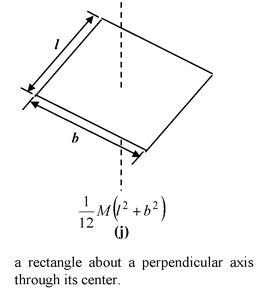
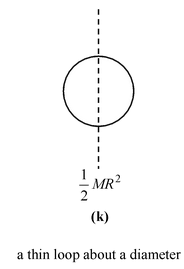
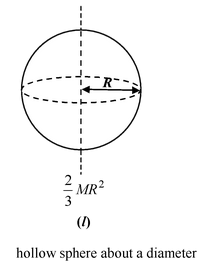
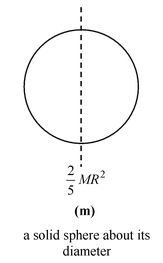
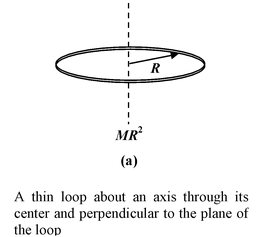
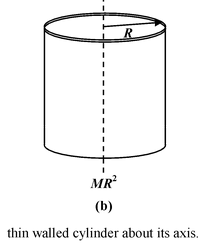
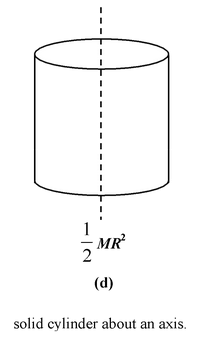
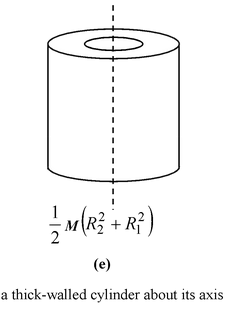
Table 10.2 Moment of Inertia of some common shaped Bodies
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

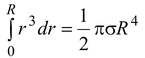
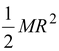 (10.19)
(10.19)
 .
.