Characteristic Property 1 (AAA Similarity)
Triangles of Class 10
THEOREM 3:
If in two triangles, the corresponding angles are equal, then the triangles are similar.
Given: Two triangles ABC and DEF in which 
.
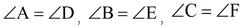To prove: ΔABC ~ ΔDEF.
Proof:
Case 1: When AB = DE
In triangles ABC and DEF, we have
∠A = ∠D [Given]
AB = DE [Given]
∠B = ∠E [Given]
∴ 
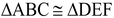[By ASA congruency]
⇒ BC = EF and AC = DF [c.p.c.t.]
Thus 
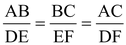[corresponding sides of similar Δs are proportional]
Hence 
Case 2: When AB < DE
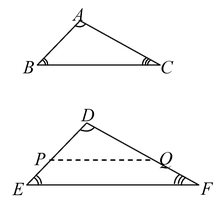
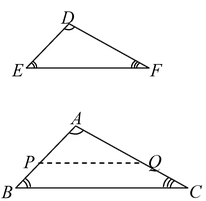
Let P and Q be points on DE and DF respectively such that DP = AB and DQ = AC. Join PQ.
In ΔABC and ΔDPQ, we have
AB = DP [By construction]
∠A = ∠D [Given]
AC =DQ [By construction]
∴ ΔABC ≅ ΔDPQ [By SAS congruency]
∴ ∠ABC = ∠DPQ [c.p.c.t.] …(i)
But ∠ABC = ∠DEF [Given] …(ii)
∴ ∠DPQ = ∠DEF [c.p.c.t.]
But ∠DPQ and ∠DEF are corresponding angles.
⇒ PQ || EF
∴ 
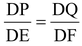[Corollary to BPT Theorem]
∴ 
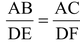. [∴ DP = AB and DQ = AC (by construction)]
Similarly 
∴ 
.
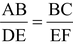
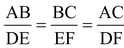Hence, ΔABC ~ ΔDEF.
|
Case 3: When AB > DE Let P and Q be points on AB and AC respectively such that AP = DE and AQ = DF. Join PQ. In ΔAPQ and ΔDEF, we have AP = DE [By construction] AQ = DF [By construction] ∠A = ∠D [Given] |
|
∴ ΔAPQ ≅ ΔDEF [By SAS congruency]
∴ ∠APQ = ∠DEF [c.p.c.t.] …(i)
But ∠DEF = ∠ABC. [Given] …(ii)
From (i) and (ii) we have
∴ ∠APQ = ∠ABC.
But ∠APQ and ∠ABC are corresponding angles
∴ PQ || BC
∴ 
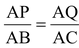[Corollary to BPT Theorem]
∴ 
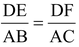[∴ AP = DE and AQ = DF (by construction)]
Similarly 
.
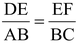Thus 
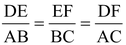
Or, 
.
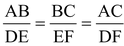Hence ΔABC ~ ΔDEF.
