Introduction
Vector of Class 11
Definition: The physical quantities specified completely by their magnitude as well as direction are called vector quantities. The magnitude and direction alone cannot decide whether a physical quantity is a vector. In addition to the above characteristics, a physical quantity, which is a vector, should follow laws of vector addition. For example, electric current has magnitude as well as direction, but does not follow laws of vector addition. Hence, it is not a vector.
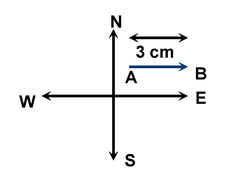
A vector is represented by putting an arrow over it. The length of the line drawn in a convenient scale represents the magnitude of the vector. The direction of the vector quantity is depicted by placing an arrow at the end of the line.
|
For example, if 1 cm length is equal to 20 km/hr, then vector
The point A is called initial point or tail and point B is called terminal point or head. |
|
If two vectors have the same direction, they are parallel. Two vectors are said to be equal when their magnitudes and directions, both are same, e.g. if
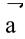 =
=
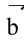 then |
then |
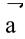 | = |
| = |
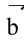 | and the directions of vectors are same. Thus, a vector is not altered by shifting it parallel to itself in the space.
| and the directions of vectors are same. Thus, a vector is not altered by shifting it parallel to itself in the space.
The vector having same magnitude as of
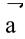 , but the opposite direction is defined as the negative or opposite of
, but the opposite direction is defined as the negative or opposite of
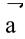 and is denoted by -
and is denoted by -
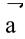 .
.
Unit vector
A vector having magnitude equal to unity. To find the unit vector in the direction of
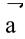 , we divide the given vector by its magnitude.
, we divide the given vector by its magnitude.
For example,
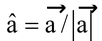 , or
, or
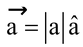 or
or
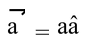 , where |
, where |
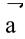 | or a is the magnitude of the vector
| or a is the magnitude of the vector
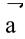 .
.
Unit vector is basically used to indicate the direction.
Null vector or zero vector
A vector having zero magnitude and indeterminate direction is called Zero or Null Vector.
Concept of zero vector is helpful in substraction of two equal magnitude vectors in opposite direction and vector product of two parallel vectors.
The concept of null vector is hypothetical but we introduce it only to explain some mathematical results.
Invariancy of the vector
Any vector is invariant so it can be taken anywhere in the space keeping its magnitude and direction same. In other words, the vector remains invariant under translation.

 represents
represents