Superposition Of Waves
Wave Motion of Class 11
Superposition Of Waves
When the amplitude of two waves travelling through the same elastic medium is small then, the instantaneous displacement of each particle of the medium is the vector sum of the displacements due to each wave. This property is called the principle of superposition.
It means that the wave do not alter one another and each propagates through the medium as if the other were not there.
This fact is evident from the Fig. (14.10).
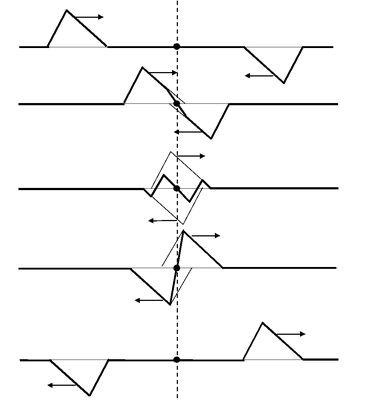
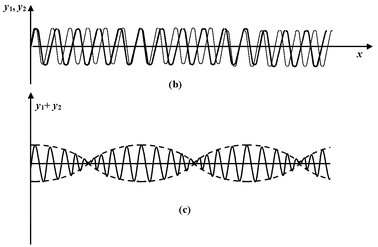
Fig.(14.10) Two wave pulses that are inverted mirror images of each other are produced at the ends of a string. As the waves pass each other, the string has a complex shape but the one point on the dashed line is always at rest. The string shape is found by adding the displacements of the two pulses at every point.
Let us begin with two waves both travelling on the same string. When we look at the wave function of either of the two waves y = A sin(kx ± ωt + φ), it is obvious that there are many ways that the two waves can differ. The waves may have opposite directions, different amplitudes A, different wavelengths, different frequencies or one wave may differ in phase from the other. Let us discuss all cases one by one.
Interference: Adding waves that differ in Phase only
Consider two waves travelling on the same string with the same amplitude, wavelength and frequency but with a constant phase difference as described by the following equations:
y1 = asin(kx - ωt)
y 2 = asin(kx - ωt + φ)
Note that the phase constant φ specifies the extent to which the second wave is shifted along the x – axis relative to the first wave. The resultant wave is obtained by superposing the two waves.
y = y 1 + y 2 = a[sin(kx - ωt) + sin(kx – ωt + φ)]
Using trigonometric identity
y = (2a cos φ/2) sin(kx- ωt - φ/2)(14.22)
The argument of the sine term in equation (14.22) indicates that we still have a wave with the same frequency and wavelength. However, the wave is phase-shifted by φ/2 relative to wave 1.
The term (2acosφ/2) is interpreted as the new amplitude of the wave. Thus, the equation (14.22) may be written as
y = A sin (kx - ωt - φ/2)
where A = 2acos(φ/2). Note that the new amplitude depends on the phase constant φ.
Constructive & Destructive Interference
When φ = 2nπ (where n = 0, 1, 2, ….), the positions of crests and troughs of each wave coincide with the positions of the crests and troughs of another wave and produce constructive interference.
A = 2acos[2nπ/2] = ±2a
Similarly, if φ = (2n – 1)π then destructive interference is produced.
A = 2acos[(2n - 1)π/2] = 0
If the two waves have different amplitudes a1 and a2, respectively, the resultant amplitude is given by
A = √a 1 2 + a 2 2 + 2a 1 a 2 cosφ(14.23)
where φ is the constant phase difference.
If φ = 2nπ where n = 0, 1, 2, ……….
Amax = a1 + a2 (constructive)
Ifφ = (2n – 1)π where n = 1, 2, 3, ……….
Amin = a 1 – a 2 (destructive)
Since intensity is proportional to the square of the amplitude. Therefore,
I = I1 + I2 + 2√I 1 I 2 cosφ
Ifφ = 2nπ where n = 0, 1, 2, …….
Imax = (√I 1 + √I 2 ) 2
Ifφ = (2n – 1)π where n = 1, 2, 3,……….
Imin = (√I 1 - √I 2 ) 2
Example 14.4
Two coherent sound sources are at distances x1 = 0.2 m and x2 = 0.48 m from a point. Calculate the intensity of the resultant wave at that point if the frequency of each wave is
f = 400 Hz and velocity of wave in the medium is v = 448 m/s. The intensity of each wave is Io = 60 W/m2.
Solution
Path difference, p = x 2 - x 1 = 0.48 - 0.2 = 0.28 m
φ = 2π/λp = (2πf/v)p = 2π(400)(0.28)/448 = π/2
I = I1 + I2 + √I 1 I 2 2cosφ
orI = Io + Io + 2Io cos(π/2) = 2Io = 2(60) = 120 W/m 2 .
Beats: Adding Wave That Differ in Frequency Only.
Consider two waves of same amplitude and phase but with slightly different frequencies f1 and f2 as described by the equations
y 1 = a sin(k 1 x - ω1t)
y 2 = a sin(k2x - ω2t)
Note that different frequencies corresponds to different wave numbers k1 = ω
1
/v and
k
2
= ω
2
/v
Using superposition principle
y = y1 + y2 =
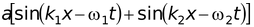
ory =
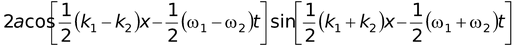 (14.24)
(14.24)
In order to intercept equation (14.24), let us see how this wave look at t = 0.
We define the average wave number
kav = k1 + k2/2
and the wave number difference
Δk = k1 – k2
At t = 0, the equation (14.24) reduces to
y = [2acos(Δkx/2)](sin k av x) (14.25)
Equation (14.25) represents a sinusoidal wave with a wave number equal to the average of the two component waves. The amplitude of this wave varies with position x as given by
A = 2acos(Δkx/2)
At x = 0 it is a maximum 2a, at xmin = π/Δk it decreases to zero, and at
xmax = 2π/Δk it again reaches a maximum.
|
|
|
|
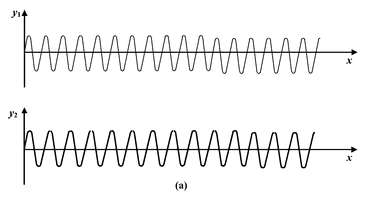
Fig.(14.11) (a) Two waves of slightly different frequencies. (b) The graphs from part (a) plotted on the same graph. (c) The superposition of two waves. |
|
As t increases from zero in equation (14.24) the whole pattern shown in Fig.(14.11) moves along the x – axis with the wave velocity. At any point in space along the wave path the wave amplitude oscillates in time from a maximum of 2A to a minimum of zero or –2A. These pulsation of the amplitude are called beats. The number of amplitude pulsations per second is called the beat frequency.
The time between amplitude maximums for a wave travelling with velocity v is
T =
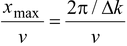
∴ beat frequency f =
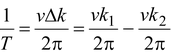
or f =
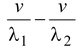
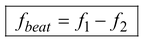 (14.26)
(14.26)
Also Check
Example 14.6
Two tuning forks P and Q when set vibrating give 4 beats per second. If a prong of the fork P is filed , the beats are reduced to 2 per second. Determine the frequency of P, if that of Q is 250 Hz.
Solution
There are four beats between P and Q, therefore the possible frequencies of P are 246 or 254 (that is 250 ± 4) Hz.
When the prong of P is filed, its frequency becomes greater than the original frequency.
If we assume that the original frequency of P is 254, then on filing its frequency will be greater than 254. The beats between P and Q will be more than 4. But it is given that the beats are reduced to 2, therefore, 254 is not possible.
Therefore, the required frequency must be 246 Hz.
(This is true, because on filing the frequency may increase to 248, giving 2 beats with Q of frequency 250 Hz.)
Example 14.7
Wavelengths of two notes in air are m and m . Each note produces four beats per second with a third note of a fixed frequency. Calculate the velocity of sound in air.
Solution
Given λ1 = mand λ2 = m.
Let f1 and f2 be the corresponding frequencies and v be the velocity of sound in air.
v = λ1 f1andv = λ2f2
∴f1 = v/λ 1 andf2 = v/λ2
Since λ2 > λ1∴f1 > f2
Let f be the frequency of the third note.
∴f1 - f = 4 andf - f2 = 4
∴f 1 - f2 = 8
∴
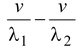 = 8
= 8
v[175/90 - 173/90] = 8
∴ v = 2/90 = 8
∴ v = 360 ms
-1
Standing Waves: Adding Waves That Differ In Direction Only
Consider two waves y 1 and y 2 that have the same amplitude, wavelength and frequency but travel in opposite directions:
y 1 = asin(kx - ωt)
y 2 = asin(kx + ωt)
Using superposition principle
y = y 1 + y 2 = a[sin (kx -ωt) + sin(kx +ωt)]
or y = 2a sin kx cos ωt (14.27)
ory = A cos ωt
whereA = 2asin kx
The equation (14.27) shows that the string executes simple harmonic motion such that every point on the string vibrates in same phase with same frequency but different amplitudes which depend on the position x of the point along the string.
This type of wave motion represented by equation (14.27) is called a standing wave because it appears to travel neither to the left nor to the right.
There are positions along the string for which the amplitude of oscillation is always zero (called nodes), and other positions where the amplitude of oscillation is always 2a (called antinodes)
Positions of Nodes
Any position for which kx is a multiple of π yields a zero; all these are the positions of nodes
kx = 0, π, 2π, 3π, …….
Since k = 2π/λ
therefore
x = 0, λ/2. 2λ/2,3λ/2 ………
Note that the distance between two successive nodes is λ/2.
Positions for which kx is an odd multiple of π/2 yields maximum value of 2asinkx; all these are the positions of antinodes.
kx = π/2, 3π/2, 5π/2……….
or x = λ/4,3λ/4, 5λ/4 …………
Note that the distance between two successive antinodes is λ/2. Also, nodes and antinodes occur alternatively and equally spaced from each other.
The sound produced from stringed musical instruments (such as violin, guitar, piano, etc.) are generated by combinations of standing waves. An important characteristic of the waves on these instruments is that both ends of the string are fixed either by the instrument itself (in the case of piano) or by the instrument at one end and a finger at the other end (in the case of guitar and violin).
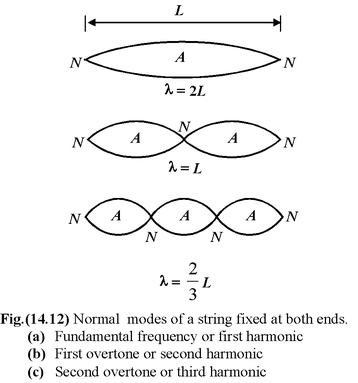
The standing wave patterns possible on the string are called the normal modes.
|
Fig.(14.12) shows that the wavelength of the normal modes must be λ = 2L, L, 2L/3,………. In general λ = 2L/n where n = 1, 2, 3……. The respective frequencies are given by Thus,f = v/2L, v/L 3v/L……. In general, f = n(v\L) where n = 1, 2, 3, …… (14.28) |
|

Example 14.10
Two wires are fixed on a sonometer. Their tensions are in the ratio 8 : 1, their lengths are in the ratio 36 : 35, the diameters are in the ratio 4 : 1 and densities are in the ratio 1 : 2. Find the frequencies of the beats produced if the note of the higher pitch has a frequency of 360 per second.
Solution
Given :
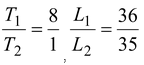
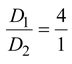 ,
,
Let f1 and f2 be the linear densities.
∴μ1 =
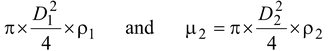
∴
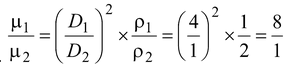
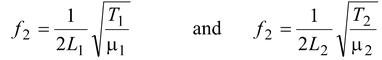
∴
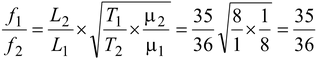
f2 > f1 , we have f2 = 360 ∴f1 = 350
Beats = f2 - f1 = 10 per second.
Example 14.11
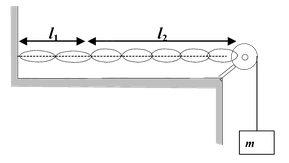
An Aluminium wire of length l1 = 60.0 cm and of cross-sectional area 0.01cm2 is connected to a steel wire of the same cross sectional area. The compound wire is loaded with a block m of mass 10 kg, as shown in the figure, so that the distance l2 from the joint to the supporting pulley is 86.6cm Transverse waves are set up in the wire by using an external source of variable frequency
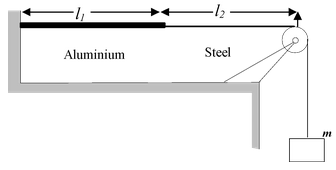
(a) Find the lowest frequency of excitation for which standing waves are observed such that the joint in the wire is a node.
(b) What is total number of nodes observed at this frequency excluding the two at the ends of the wire ?
Density of aluminium is 2.6 g/cm3 ; Density of steel is 7.8 g/cm3
Solution
The distance between two nodes is equal to λ/2. The whole wire vibrates with the frequency of the tuning fork. But as the velocity of the wave in each part of the wire is √T/μ not be different.
Let the aluminium wire vibrates in n1 harmonics and the steel wire vibrates in n2 harmonics.
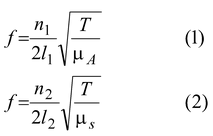
l1 = 60.0 cm.
Area of cross section = 1.00 × 10-2 cm2. Density of Aluminium = 2.6 gm/cm3
μA = (2.6)(1 × 102) = 0.026 g/cm ; μs = (7.8)(1 × 102) = 0.078 g/cm.
Equating (1) and (2) we get,
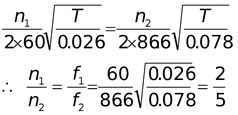
∴ The lowest frequency of excitation causes n1 = 2 and n2 = 5.
Thus the frequency =
The vibrating wire looks as shown in the figure.