Formula For Root Mean Square Speed of Gas Molecules

May 01, 2022, 16:45 IST

Root mean Square (C_rms) speed :

The fraction of molecules having either very high or very low speeds is very small. Majority of molecules have speed near to C_rms in the middle of the range of molecular speeds. The total area under the curve in Figure is a measure of total number of molecules in collection.

It is denoted by C_rms = root square mean value

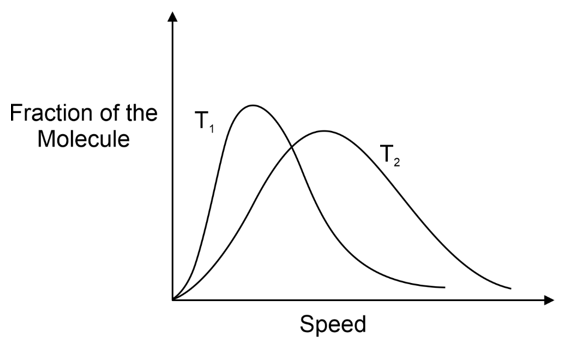
Since, rise in temperature raises the kinetic energy of gas molecules, it follows that fractions of molecules having lower speed range decreases and fraction of molecules having higher speed range increases. Also the curve at higher temperature has its u_mps shifted to higher value but the corresponding fractions of molecules have decreased. Thus in general, the distribution of speeds is wider at higher temperature than at lower temperature as shown in figure (T₂ > T₁)

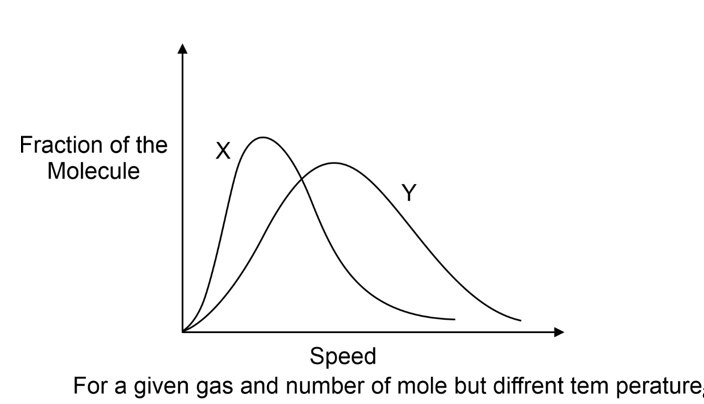
Distribution of molecular speed also depends upon the mass of gas molecule. At similar temperature, a heavier gas molecule has a narrow distribution of speeds than a lighter gas molecule as shown in the following diagram (M_X > M_Y):

As per kinetic theory of gases, each molecule is moving with altogether different velocity. Let ‘n’ molecules be present in a given mass of gas, in which n1 molecules have a speed of v₁, n₂ molecules have a speed of v₂, ,n_n molecules have a speed of v_n.

Root mean Square (C_rms) speed formulas

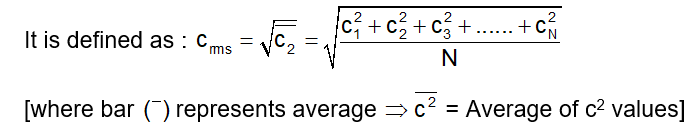
Since the distribution is continuous, we can write :

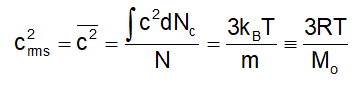
Where M_o = Mol. Mass of the gas (in kg)

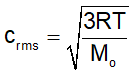
Derivations of Root mean Square

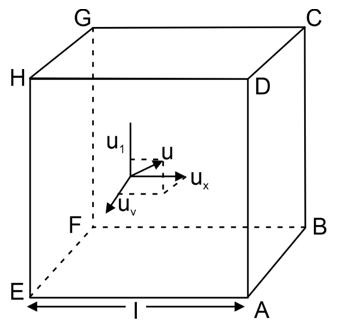
Imagine a cube of edge-length l, containing N molecules, each having a mass of m. Molecules are moving at random in all directions, with speed covering a considerable range of values. The velocity u₁ of any molecule may be resolved into three- component velocities designated as u_x, u_y and u_z., These are in the three directions at right angles to each other and parallel to the sides of the cube as shown in figure. The component velocities are related by the expression 

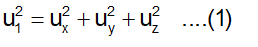
Considering the x-component motion of a molecule, we will have Momentum of molecule before collision with the side ABCD = mu_x.

Momentum of the molecule after collision with the side ABCD = –mu_x.

Change of momentum of the molecule in a single collision with the side ABCD = |2mu_x|. Since l is the edge length of the cube, the molecule has to travel a distance 2l to arrive back at the wall ABCD. The number of collisions per unit time with the wall ABCD will be equal to u_x/2l.

The total change of momentum per unit time due to such impacts is 

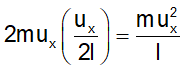
According to Newton’s second law of motion

Force = mass × acceleration 

mass x d(velocity)/dt

= d/dt (mass x velolcity)

= d/dt(momentum = rate of change of momentum

Hence, total force due to impacts of a single molecule with the wall ABCD of the vessel is Mu_x²/l. The area of the wall is l². Hence, the pressure exerted due to the collision of x-component velocity of a single molecule with the side ABCD is

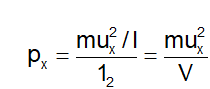
where V is the volume of the vessel

Since each molecule will exert similar pressure, the total pressure exerted on the wall ABCD will be

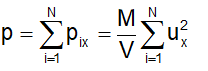
Defining the mean square speed as 

Since the directions x, y and z are equivalent, we will also have 

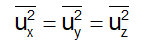
But from Eq. (1), we will have 

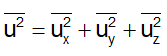
From Eqs (1) and (3), we can write 

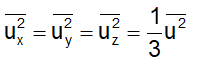
Substituting this in Eq. (2), we get 

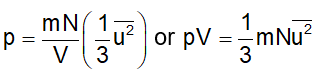
From Maxwell distribution we already know 

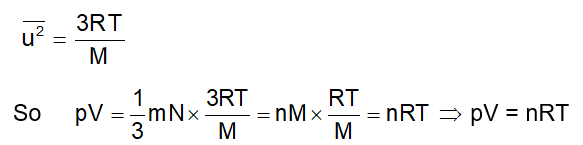
• Average translational kinetic  = ½ mu_rms²  = 3/2kT energy per molecule
• Average Translational Kinetic = N_A × ½ mu_rms² = 3/2RT energy per mole
• k(Boltzmann constant) = R/N_A = 1.38 × 10^–23 JK^–1