
NCERT Solution for class 8 maths chapter 11 Mensuration
NCERT Solutions for Class 8 Maths Mensuration
NCERT Solutions for Class 8 Maths Exercise 11.1
Question 1.
A square and a rectangular field with measurements as given in the figure have the same perimeter.
Which field has a larger area? 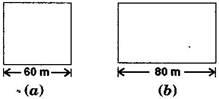
Solution :
Given: The side of a square = 60 m
And the length of rectangular field = 80 m
According to question,
Perimeter of rectangular field
= Perimeter of square field 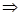
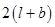 = 4
= 4 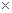 side
side 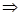
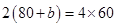
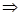
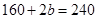
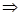
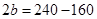
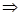
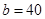 m
m
Now Area of Square field
= 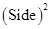
= = 3600 m 2
And Area of Rectangular field
= length  breadth = 80
breadth = 80  40
40
= 3200
Hence, area of square field is larger.
Question 2.
Mrs. Kaushik has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of ` 55
per m 2 . 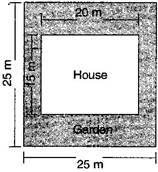
Solution : Side of a square plot = 25 m  Area of square plot =
Area of square plot = 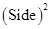
= 625 m 2
Length of the house = 20 m and 
Breadth of the house = 15 m
Area of the house = length breadth
= 20 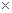 15 = 300 m 2
15 = 300 m 2 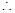 Area of garden = Area of square X plot
Area of garden = Area of square X plot
– Area of house
= 625 – 300 = 325 m 2
∵ Cost of developing the garden per sq. m = ` 55
∴ Cost of developing the garden 325 sq. m = ` 55 325
= ` 17,875
Hence total cost of developing a garden around is ` 17,875.
Question 3.
The shape of a garden is rectangular in the middle and semi-circular at the ends as shown in the diagram. Find the area and the perimeter of this garden [Length of rectangle is 20 – (3.5 + 3.5 meters] 
Solution :
Given: Total length = 20 m
Diameter of semi circle = 7 m
∴ Radius of semi circle = 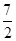 = 3.5 m
= 3.5 m
Length of rectangular field
= 20 – (3.5 + 3.5) = 20 – 7 = 13 m
Breadth of the rectangular field = 7 m
Area of rectangular field = l 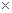 b
b
= 13 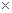 7 = 91 m²
7 = 91 m²
Area of two semi circles = 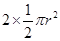
= 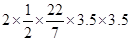 = 38.5 m 2
= 38.5 m 2
Area of garden = 91 + 38.5 = 129.5 m 2
Now Perimeter of two semi circles = 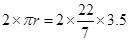 = 22 m
= 22 m
And Perimeter of garden
= 22 + 13 + 13
= 48 m
Question 4.
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m 2 ? [If required you can split the tiles in whatever way you want to fill up the corners]
Solution :
Given: Base of flooring tile = 24 cm
= 0.24 m
Corresponding height of a flooring tile
= 10 cm = 0.10 m
Now Area of flooring tile
= Base × Altitude
= 0.24 × 0.10
= 0.024 m 2
Number of tiles required to cover the floor
= 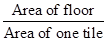
= 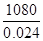
= 45000 tiles
Hence 45000 tiles are required to cover the floor.
Question 5.
An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression c = 2πr where r is the radius of the circle. 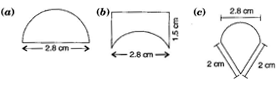
Solution :
(a) Radius = 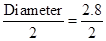
= 1.4 cm
Circumference of semi circle = πr
= 22/7 × 1.4 = 4.4 cm
Total distance covered by the ant
= Circumference of semi circle + Diameter
= 4.4 + 2.8 = 7.2 cm
(b) Diameter of semi circle = 2.8 cm 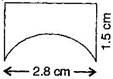
![]() Radius =
Radius = 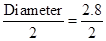 = 1.4 cm
= 1.4 cm
Circumference of semi circle = πr
= 22/7 × 1.4 = 4.4 cm
Total distance covered by the ant
= 1.5 + 2.8 + 1.5 + 4.4 = 10.2 cm
(c) Diameter of semi circle = 2.8 cm 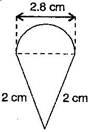
Radius = 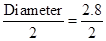
= 1.4 cm
Circumference of semi circle = πr
= = 4.4 cm
Total distance covered by the ant
= 2 + 2 + 4.4 = 8.4 cm
Hence for figure (b) food piece, the ant would take a longer round.
NCERT Solutions for Class 8 Maths Exercise 11.2
Question 1.
The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m. 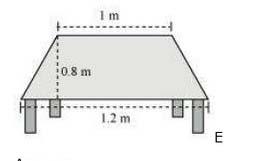
Solution :
Here one parallel side of the trapezium (a) = 1 m
And second side (b) = 1.2 m and
height (h) = 0.8 m
Area of top surface of the table
= 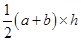 =
= 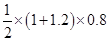
= 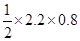 = 0.88 m 2
= 0.88 m 2
Hence surface area of the table is 0.88
Question 2.
The area of a trapezium is 34 cm² and the length of one of the parallel sides is 10 cm and its height is 4 cm. 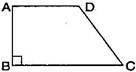
Find the length of the other parallel side.
Solution :
Let the length of the other parallel side be b.
Length of one parallel side (a) = 10 am and height (h) = 4 cm
Area of trapezium = 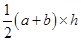
![]()
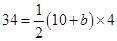
![]()
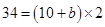
![]()
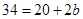
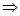 34 -20 = 2b
34 -20 = 2b 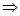 14 = 2b
14 = 2b 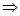 7 = b
7 = b 
![]()
Hence another required parallel
side is 7 cm.
Question 3.
Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC. 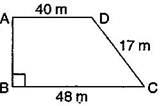
Solution :
Given: BC = 48 m, CD = 17 m,
AD = 40 m and perimeter = 120 m
∵ Perimeter of trapezium ABCD
= AB + BC + CD + DA
120 = AB + 48 + 17 + 40
120 = AB = 105 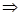 AB = 120 – 105 = 15 m
AB = 120 – 105 = 15 m
Now Area of the field
= 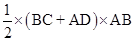
= 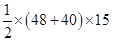
= 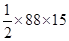
= 660 m²
Hence area of the field ABCD is 660.
Question 4.
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field. 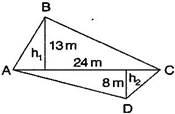
Solution :
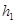 = 13 m,
= 13 m, 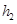 = 8 m and
= 8 m and
AC = 24 m
Area of quadrilateral ABCD
= Area of ![]() ABC + Area of
ABC + Area of ![]() ADC
ADC
= 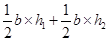
= 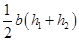
= 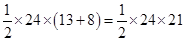
=252 m²
Hence required area of the field
is 252 m²
Question 5.
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Solution :
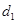 =7.5 cm and
=7.5 cm and 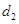 = 12 cm
= 12 cm
We know that,
Area of rhombus = 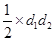
= 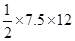
= 45 cm²
Hence area of rhombus is 45 .
Question 6.
Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of the diagonals is 8 cm long, find the length of the other diagonal.
Solution :
Since rhombus is also a kind of parallelogram.
∴ Area of rhombus
= Base ×Altitude
= 6 × 4 = 24
Also Area of rhombus = 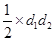
![]() 24 =
24 = 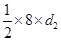
![]()
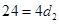
![]()
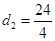 = 6 cm
= 6 cm
Hence the length of the other
diagonal is 6 cm.
Question 7.
The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m² is ` 4.
Solution :
Here, 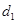 = 45 cm and
= 45 cm and 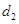 = 30 cm
= 30 cm
Area of one tile = 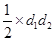
= 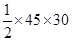 = 675 cm²
= 675 cm² ![]() Area of 3000 tiles
Area of 3000 tiles
= 675 × 3000 = 2025000 cm²
= 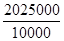
= 202.50 ![]()
∵ Cost of polishing the floor per
sq. meter = 4
∴ Cost of polishing the floor per 202.50 sq. meter = 4 202.50 = 810
Hence the total cost of polishing the floor is 810.
Question 8.
Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the sidealong the road. If the area of this field is 10500 m 2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river. 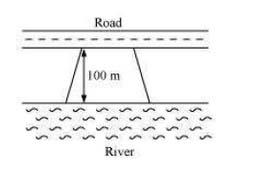
Solution :
Given: Perpendicular distance (h)
= 100 m
Area of the trapezium shaped field
= 10500 m²
Let side along the road be x m and side along the river = 2x m ![]() Area of the trapezium field
Area of the trapezium field
= 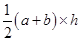
![]() 10500 =
10500 = 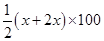
![]()
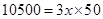
![]()
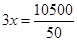
![]()
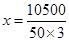
![]()
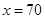 m
m
Hence the side along the river =2x
= 2 × 70 = 140 m.
Question 9.
Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface. 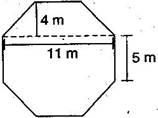
Solution :
Given: Octagon having eight equal sides, each 5 m. Construction: Divided the octagon in 3 figures, two trapeziums whose parallel and perpendicular sides are 11 m and 4 m respectively and third figure is rectangle having length and breadth 11 m and 5 m respectively. 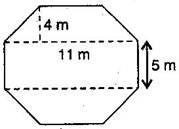
Now Area of two trapeziums = 2 x 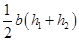
= 2 × 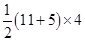 = 4 × 16 = 64
= 4 × 16 = 64
And Area of rectangle = length breadth
= 11 × 5 = 55m 2
∴ Total area of octagon = 64 + 55
= 119
Question 10.
There is a pentagonal shaped park as shown in the figure.
For finding its are a Jyoti and Kavita divided it in two different ways. 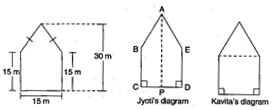
Find the area of this park using both ways. Can you suggest some other way of finding its area?
Solution :
First way: By Jyoti’s diagram,
Area of pentagon = Area of trapezium ABCP + Area of trapezium AEDP
= 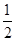 (AP + BC) x CP +
(AP + BC) x CP + 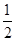 (ED + AP) DP =
(ED + AP) DP = 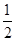 (30 + 15 ) x CP +
(30 + 15 ) x CP + 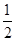 (15 + 30) DP
(15 + 30) DP
= 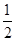 (30 + 15) (CP + DP)
(30 + 15) (CP + DP)
= 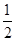 45 × C × D
45 × C × D 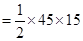
=337.5 m 2
Second way:
By Kavita’s diagram
Here, a perpendicular AM drawn to BE.
AM = 30 – 15 = 15 m
Area of pentagon
= Area of Δ ABE + Area of square BCDE 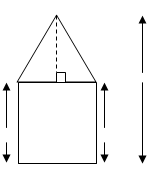
=  15 x 15+15 x 15m
15 x 15+15 x 15m
= 112.5 + 225.0
= 337.5 m 2
Hence total area of pentagon shaped
park = 337.5. m²
Question 11.
Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of theframe, if the width of each section is same. 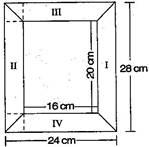
Solution :
Here two of given figures (I) and (II) are similar in dimensions.
And also figures (III) and (IV) are similar in dimensions.
∴ Area of figure (I) = Area of trapezium
= 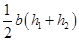
= 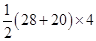
= 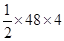
= 96 cm²
Also Area of figure (II) = 96 cm 2
Now Area of figure (III)
= Area of trapezium = 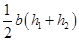
= 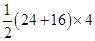 =
= 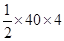 = 80 cm 2
= 80 cm 2
Also Area of figure (IV) = 80 cm 2
NCERT Solutions for Class 8 Maths Exercise 11.3
Question 1.
There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make? 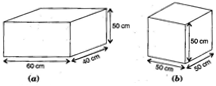
Solution :
(a) Given: Length of cuboidal box (l) = 60 cm
Breadth of cuboidal box (b) = 40 cm
Height of cuboidal box (h) = 50 cm
Total surface area of cuboidal box
= [ 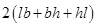 ]
]
= 2 (60 x 40 + 40 x 50 + 50 x 60)
= 2 (2400 + 2000 + 3000
= 2 x 7400 = 14800
(b) Given: Length of cuboidal box (l)
= 50 cm
Breadth of cuboidal box (b) = 50 cm
Height of cuboidal box (h) = 50 cm
Total surface area of cuboidal box
= 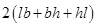
= 2 (50 50 + 50 50 + 50 50)
= 2 (2500 + 2500 + 2500)
= 2 × 7500 = 15000 cm 2
Hence cuboidal box (a) requires the lesser amount of materal to make, since surface area of box is less than that of box
Question 2.
A suitcase with measures 80 cm × 48 cm × 24 cm is to be covered with a tarpaulin cloth. How many meters of tarpaulin of width 96 cm is required to cover 100 such suitcases?
Solution :
Given: Length of suitcase box (l) = 80 cm, Breadth of suitcase box (b) = 48 cm
And Height of cuboidal box = 24 cm
Total surface area of suitcase box
= 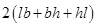
= 2 (80 × 48 + 48 × 24 + 24 × 80)
= 2 (3840 + 1152 + 1920)
= 2 × 6912 = 13824
Area of Tarpaulin cloth = Surface area of suitcase ![]() = 13824
= 13824 ![]()
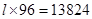
![]()
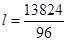 = 144 cm
= 144 cm
Required tarpaulin for 100 suitcases
= 144 100 = 14400 cm = 144 m
Hence tarpaulin cloth required to cover 100 suitcases is 144 m.
Question 3.
Find the side of a cube whose surface area id 600 cm 2
Solution :
Here Surface area of cube = 600 cm 2 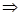
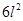 = 600
= 600 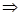
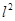 = 100
= 100 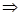 l = 10 cm
l = 10 cm
Hence the side of cube is 10 cm
Question 4.
Rukshar painted the outside of the cabinet of measure 1 m ×2 m × 1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet? 
Solution :
Here, Length of cabinet (l) = 2 m, Breadth of cabinet (b) = 1 m
And Height of cabinet (h) = 1.5 m
Surface area of cabinet =
= 2 × 1 + 2 (1 × 1.5 + 1.5 × 2)
= 2 + 2 (1.5 + 3.0)
= 2 + 9.0
= 11m²
Hence required surface area of cabinet is 11.
Question 5.
Daniel is paining the walls and ceiling of a cuboidal hall with length, breadth and height of 15 m, 10 m and 7 m respectively. From each can of paint 100 m² of area is painted. How many cans of paint will she need to paint the room?
Solution :
Here, Length of wall (l) = 15 m, Breadth of wall (b) = 10 m
And Height of wall (h) = 7 m ![]() Total Surface area of classroom
Total Surface area of classroom
= 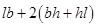
= 15 × 10 + 2 (10 × 7 + 7 × 15)
= 150 + 2 (70 + 105)
= 150 + 350
= 500 m²
Now Required number of cans
= 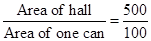 = 5 cans
= 5 cans
Hence 5 cans are required to paint the room.
Question 6.
Describe how the two figures below are alike and how they are different. Which box has larger lateral surface area? 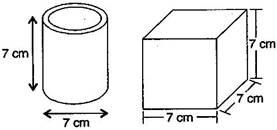
Solution :
Given: Diameter of cylinder = 7 cm
Radius of cylinder (r) = ![]() cm
cm
And Height of cylinder (h) = 7 cm
Lateral surface area of cylinder = 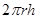
= 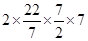
= 154 cm 2
Now lateral surface area of cube
= 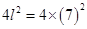 = 4 × 49 = 196 cm²
= 4 × 49 = 196 cm²
Hence the cube has larger lateral surface area.
Question 7.
A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How much sheet of metal is required? 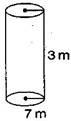
Solution :
Given: Radius of cylindrical tank (r)= 7 m
Height of cylindrical tank (h) = 3 m
Total surface area of cylindrical tank
= 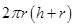
= 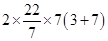
= 44 × 10 = 440 m²
Hence 440 metal sheet is required.
Question 8.
The lateral surface area of a hollow cylinder is 4224 cm² . It is cut along its height and formed a rectangular sheet of width 33 cm. Find the perimeter of rectangular sheet?
Solution :
Given: Lateral surface area of hollow cylinder = 4224 cm²
And Height of hollow cylinder = 33 cm
Curved surface area of hollow cylinder = 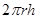
![]() 4224 =
4224 = 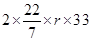
![]()
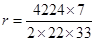 =
= 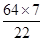 cm
cm
Now Length of rectangular sheet = 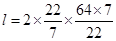 = 128 cm
= 128 cm
Perimeter of rectangular sheet = 2(l + b)
= 2 (128 + 33) = 2 x 161 = 322 cm
Hence perimeter of rectangular sheet is 322 cm.
Question 9.
A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and length 1 m. 
Solution :
Given: Diameter of road roller = 84 cm
Radius of road roller 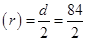
= 42 cm
Length of road roller (h) = 1 m = 100 cm
Curved surface area of road roller = 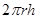 =
= 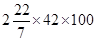 = 26400 cm2
= 26400 cm2
Area covered by road roller in 750 revolutions = 26400 750
= 1,98,00,000 cm²
= 1980 m² [ 1 m²= 10,000 cm²]
Hence the area of the road is 1980.m²
Question 10.
A company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm. Company places a label around the surface of the container (as shown in figure). If the label is placed 2 cm from top and bottom, what is the area of the label? 
Solution :
Given: Diameter of cylindrical container = 14 cm
Radius of cylindrical container 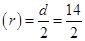 = 7 cm
= 7 cm
Height of cylindrical container = 20 cm
Height of the label (h) = 20 – 2 – 2
= 16 cm
Curved surface area of label = 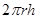
= = 704 cm 2
Hence the area of the label of 704 cm 2.
NCERT Solutions for Class 8 Maths Exercise 11.4
Question 1.
Given a cylindrical tank, in which situation will you find surface are and in which situation volume.
(a) To find how much it can hold.
(b) Number of cement bags required to plaster it.
(c) To find the number of smaller tanks that can be filled with water from it.
Solution :
We find area when a region covered by a boundary, such as outer and inner surface area of a cylinder, a cone, a sphere and surface of wall or floor.
When the amount of space occupied by an object such as water, milk, coffee, tea, etc., then we have to find out volume of the object.
(a) Volume (b) Surface area (c) Volume
Question 2.
Diameter of cylinder A is 7 cm and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area.
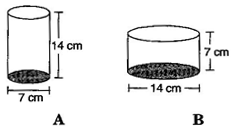
Solution :
Yes, we can say that volume of cylinder B is greater, since radius of cylinder B is greater than that of cylinder A (and square of radius gives more value than previous).
Diameter of cylinder A = 7 cm
Radius of cylinder A = cm
And Height of cylinder A = 14 cm
Volume of cylinder A = 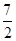
= 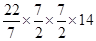
= 539
Now Diameter of cylinder B = 14 cm
Radius of cylinder B =14/2 = 7 cm
And Height of cylinder B = 7 cm
Volume of cylinder A = 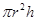
= 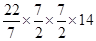
= 1078 cm³
Total surface area of cylinder A
= 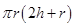 [ ∵ It is open from top]
[ ∵ It is open from top]
= 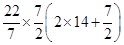
= 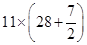
= 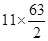 = 346.5 cm 2
= 346.5 cm 2
Total surface area of cylinder B
= 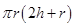 [ It is open from top]
[ It is open from top]
= 22/7 × 7 × (2 ×7 + 7)
= 22 ×(14 + 7) = 22 × 21 = 462cm²
Yes, cylinder with greater volume also has greater surface area.
Question 3.
Find the height of a cuboid whose base area is 180cm² and volume is 900cm³
Solution :
Given: Base area of cuboid = 180 cm² and Volume of cuboid = 900 cm³
We know that, ![]() Volume of cuboid = l × b × h
Volume of cuboid = l × b × h ![]() 900=180
900=180 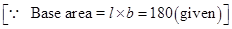
![]()
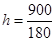 = 5 m
= 5 m
Hence the height of cuboid is 5 m.
Question 4.
A cuboid is of dimensions 60 cm 54 cm ![]() 30 cm. How many small cubes with side 6 cm can be placed in the given cuboid?
30 cm. How many small cubes with side 6 cm can be placed in the given cuboid?
Solution :

Question 5.
Find the height of the cylinder whose volume if 1.54 m 2 and diameter of the base is 140 cm.
Solution :

Question 6.
A milk tank is in the form of cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of milk in liters that can be stored in the tank. 
Solution :
Question 7.
If each edge of a cube is doubled,
(i) how many times will its surface area increase?
(ii) how many times will its volume increase?
Solution :
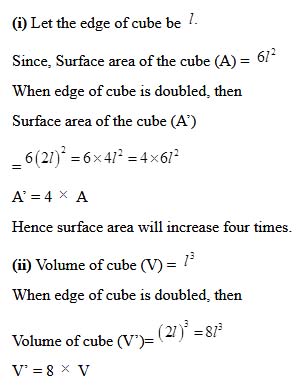
Hence volume will increase 8 times.
Question 8.
Water is pouring into a cuboidal reservoir at the rate of 60 liters per minute. If the volume of reservoir is 108, find the number of hours it will take to fill the reservoir.
Solution :










