Conditions For Solvability (Or Consistency) Of System Of Equation
Pair Of Linear Equations In Two Variables of Class 10
UNIQUE SOLUTION:
Two lines a1 + b1y + c1 = 0 and a2x + b0y + c2 = 0, if the denominator a1b2 – a2b1 ≠ 0 then the given system of equations has unique solution (i.e. only one solution) and the solutions are said to be consistent.
∴ a1b2 – a2b1 ≠ 0
⇒ 
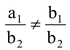
Question 1. Find the value of ‘P’ for which the given system of equations has only one solution (i.e. unique solution).
Px – y = 2 ....(i)
6x – 2y = 3 ....(ii)
Solution: a1 = P, b1 = –1, c1 = –2
a1 = 6 b2 = –2, c2 = –3.
Conditions for unique solution is
⇒ 
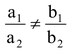
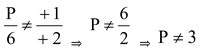
∴ P can have all real values except 3.
NO SOLUTION:
Two lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, if the denominator a1b2 – a2b1 = 0 then the given system of equations has no solution and solutions are said to be consistent.
∴ 
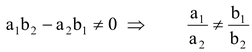
Question 1. Determine the value of k so that the following linear equations has no solution.
(3x + 1) x + 3y - 2 = 0
(k2 + 1) x + (k - 2) y – 5 = 0.
Sol. Here a1 = 3k + 1, b1 = 3 and c1 = –2
a2 = k2 + 1, b2 = k – 2 and c2 = –5
For no solution, condition is
.
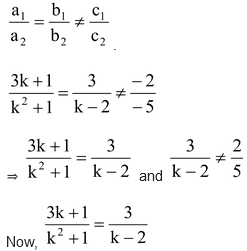⇒ (3k + 1) (k – 2) = 3(k2 + 1)
⇒ 3k2 – 5k – 2 = 3k2 + 3
⇒ –5k – 2 = 3
⇒ –5k = 5
⇒ k = –1
Clearly, 3/k - 2 ≠ 2/5 for k = –1.
Hence, the given system of equations will has no solution for k = - 1.
MANY SOLUTION (INFINITE SOLUTIONS):
Two lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, if 
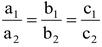then system of equations has many solution and solutions are said to be consistent.
Question 1. Find the value of k for which the system of linear equation
kx + 4y = k – 4
16x + ky = k has infinite solution.
Solution: a1 = k, b1 = 4, c1 = –(k – 4)
a2 = 16, b2 = k, c2 = – k.
Here condition is
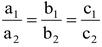
⇒ k/16 = 4/k = (k - 4)/(k)
⇒ k/16 = 4/k also 4/k = k - 4/k
⇒ k2 = 64 ⇒ 4k = k2 – 4k
⇒ k = ± 8 ⇒ k(k – 8) = 0.
k = 0 or k = 8 but k = 0 is not possible otherwise equation will be one variable.
∴ k = 8 is correct value for infinite solution.
