Equation Reducible To A Pair Of Linear Equations

We shall discuss the solution of such pairs of equations which are not linear but can be reduced to linear form by making some suitable substitutions.

question 1. Solve the following system of equations

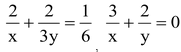,  x, y ≠ 0.

Solution: Put 1/x = u and 1/y = v

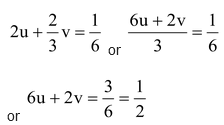
⇒ 12u + 4v = 1 …(i)

3u + 2v = 0 …(ii)

Multiply equation (ii) by 4 to make coefficients of u equal

12u + 4v = 1…(iii)

12u + 8v = 0 …(iv)

–4v = 1

v = -1/4

Putting value of v in equation (i)

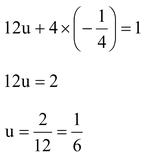
Hence,

1/x = u or 1/x = 1/6  ⇒ x = 6

1/y = v  or 1/y = 1/-4  ⇒ y = –4

Solution is x = 6, y = –4.

question 2. Solve the following system of equations

.

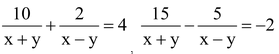Solution:

10/ x + y + 2/x- y = 4…(i)

15/x + y - 5/x -y = -2 …(ii)

Put 1/x + y = u and 1/x - y = v

10u + 2v = 4 …(iii)

15u - 5v = -2…(iv)

Multiplying equation (iii) by 5 and equation (iv) by 2 to eliminate v

50u + 10v = 20

30u - 10v = -4

80u = 16

u = 16/80 = 1/5

Putting value of u in equation (iii), we get

10 x 1/5 + 2v = 4

2 + 2v = 4

2v = 2

v = 1

∴ 1/x + y = 1/5, 1/x -y = 1

or x + y = 5 …(v)

x - y = 1 …(vi)

Adding equation (v) and (vi), we get

2x = 6 ⇒ x = 3

Putting value of x in equation (v), we get

3 + y = 5

y = 2

Solution is x = 3; y = 2

WORD PROBLEMS:

For solving daily life problems with the help of simultaneous linear equation in two variables or equations reducible to them proceed as:-

(i) Represent the unknown quantities by the same variables x and y, which are to be determined.

(ii) Find the conditions given in the problem and translate the verbal conditions into a pair of simultaneous linear equation.

(iii) Solve these equations & obtain the required quantities with appropriate units.

Type of Problems:

(i) Determining two numbers when the relation between them is given.

(ii) Problems regarding fractions, digits of number ages of persons.

(iii) Problems regarding current of a river, regarding time & distance.

(iv) Problems regarding menstruation and geometry.

(v) Problems regarding time & work.

(vi) Problems regarding mixtures, cots of articles, porting & loss, discount.

question 3. The sum of digits of a two digits number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.

Solution: Let digit at units place = y.

Let digit at tens place = x.

∴ Given number is 10x + y.

According to question,

x + y = 9 …(i)

When the digits are reversed, y becomes tens digit and x becomes units digit.

∴ Reverse number is 10y + x.

According to question,

9(10x + y) = 2(10y + x)

90x + 9y = 20y + 2x

90x - 2x = 20y - 9y

88x - 11y = 0

8x – y = 0 …(ii)

8x = y …(iii)

Putting value of y in equation (ii), we have

 x + 8x = 9

9x = 9

x = 1.

From equation (iii) y = 8.

Required number is 18.

question 4. Find two numbers such that the sum of twice the first and thrice the second is 89 and four times the first exceeds five times the second by 13.

Solution: Let the two numbers be x and y.

Then equations formed are 2x + 3y = 89 ....(i)

4x – 5y = 13 ...(ii)

On solving eq. (i) & (ii), we get

x = 22

and y = 15

Hence required numbers are 22 & 15.

question 5. The numerator of a fraction is 4 less than the denominator. If the numerator is decreased and the denominator is increased by 1, then the denominator is eight time the numerator. Find the reaction.

Solution: Let the numerator and denominator of a fraction be x and y.

Then equations formed are y – x = 4 ....(i)

y + 1 = 8 (x – 2) ....(ii)

On solving eq. (i) & (ii), we get

x = 3

and y = 7.

Hence the fraction is 3/7.

question 6. Ramesh travels 760 km to his home partly by train and partly by car. He takes 8 hours, if he travels 160 km by train and the rest by car. He takes 12 minutes more, if he travels 240 km by train and the rest by car. Find the speed of the train and the car.

Solution: Let speed of the train be x km/hr & car be y km/hr respectively.

According to the problem

160/x + 600/y = 8....(i)

240/x + 520/y = 41/5 ....(ii)

Solving equation (i) & (ii), we gets x = 80 and y = 100.

Hence, speed of the train = 80 km/hr and that of car = 100km/hr.

Do follow NCERT Solutions for Class 10 Maths prepared by expert faculty of Entrancei.