Graphical Method
Pair Of Linear Equations In Two Variables of Class 10

GRAPHICAL SOLUTION OF LINEAR EQUATIONS IN TWO VARIABLES:
Graphs of the type (i) ax = b:
question 1. Draw the graphs of the following equations:
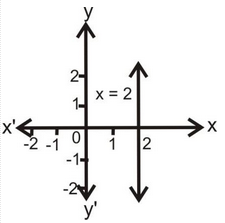
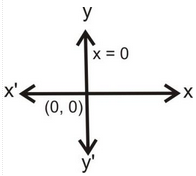
(i) x = 2, (ii) 2x = 1 (iii) x + 4 = 0 (iv) x = 0
Solution:
|
(i) x = 2 |
|
|
(ii) 2x = 1 ⇒ x = 1/2 |
|
|
(iii) x + 4 = 0 ⇒ x = –4 |
|
|
(iv) x = 0 |
|
Graphs of the type (ii) ay = b:
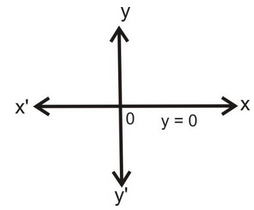
1. Draw the graphs of the following equations: (i) y = 0, (ii) y - 2 = 0, (iii) 2y + 4 = 0
|
(i) y = 0 |
|
|
(ii) y – 2 = 0 |
|
|
(iii) 2y + 4 = 0 ⇒ y = –2 |
|
Graphs of the type (iii) ax + by = 0 (Passing through origin):
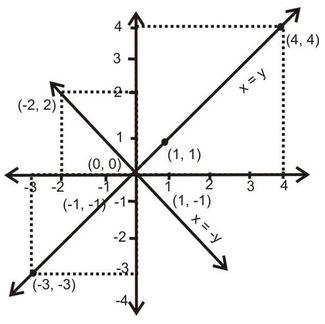
question 1. Draw the graphs of the following: (i) x = y, (ii) x = –y
Solution: (i) x – y
|
x |
1 |
4 |
–3 |
0 |
|
y |
1 |
4 |
–3 |
0 |
(ii) x = –y
|
x |
1 |
–2 |
0 |
|
y |
–1 |
2 |
0 |
Graphs of the Type (iv) ax + by + c = 0. (Making Interception x - axis, y-axis):
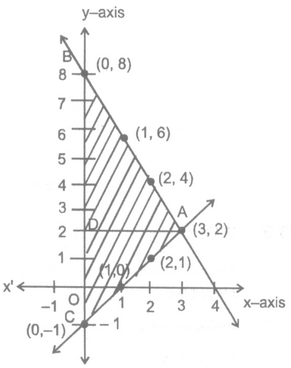
question 1. Solve the following system of linear equations graphically: x - y = 1, 2x + y = 8. Shade the area bounded by these two lines and y-axis. Also determine this area.
Solution: (i) x – y = 1
x – y + 1
|
x |
0 |
1 |
2 |
|
y |
–1 |
0 |
1 |
(ii) 2x + y = 8
(ii) 2 x + y = 8
y = 8 – 2x
|
X |
0 |
1 |
2 |
|
Y |
8 |
6 |
4 |
Solution is x = 3 and y = 2
Area of is x = 3 and y = 2
Area of ΔABC = 1/2 × BC × AD
= 1/2 × 9 × 3 = 13.5 Sq. unit.
NATURE OF GRAPHICAL SOLUTION:
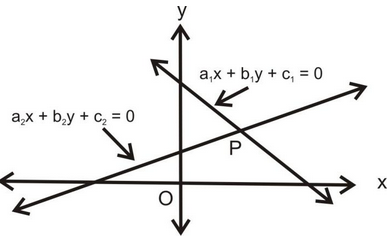
Let equations of two lines are a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0.
(i) Lines are consistent (unique solution) i.e. they meet at one point condition is .png) .
.
(ii) Lines are inconsistent (no solution) i.e. they do not meet at one point condition is 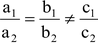 .
.
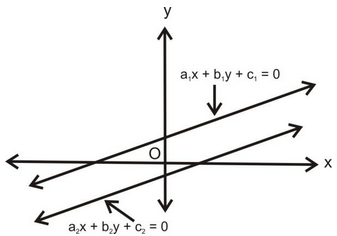
(iii) Lines are coincident (infinite solution) i.e. overlapping lines (or they are on one another) condition is .png) .
.