Free Fall
Kinematics of Class 11
Motion that occurs solely under the influence of gravity is called free fall.
In the absence of air resistance all falling bodies have the same acceleration due to gravity, regardless of their sizes or shapes.
The value of the acceleration due to gravity depends on both latitude and altitude. It is approximately 9.8 m/s 2
The equations of kinematics may be modified as
|
v = v 0 −gt(7.9) y = y 0 + 1/2 v 0 + v) t(7.10) y = y 0 + v 0 t −1/2 gt 2 (7.11)
v
2
The signs of v and v0are determined by their directions relative to the chosen +y Note : Acceleration going up or coming down. |
|
Example 7.8
A ball thrown up from the ground reaches a maximum height of 20 m. Find
(a) its initial velocity
(b) the time taken to reach the highest point
(c) its velocity just before hitting the ground
(d) its displacement between 0.5 and 2.5 s
(e) the time at which it is 15 m above the ground.
Solution
|
A coordinate system is shown in figure. Note that at the highest point the ball is instantaneously at rest, that is v (a) Given: y0= 0; y = 20 m; v = 0; a = −10 m/s2 Unknown:v 0 = ? t = ? Both equations (7.9), (7.10)(7.11)t. So from equation (7.12), |
|
0 =
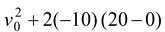
Thus,
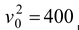 m
2
/s
2
, and v
0
= ± 20 m/s. Since “up” is positive, v
0
= + 20 m/s
m
2
/s
2
, and v
0
= ± 20 m/s. Since “up” is positive, v
0
= + 20 m/s
(b) Given:v 0 = 20 m/s
Unknown :t
Either Equation (7.9)(7.11) would lead to t. Since equation (7.11) involves a quadratic it is quicker to use equation (7.9)
0 = 20 −t
Thus t = 2 s
(c) Given: y0= 0; y = 0; vo=20 m/s
Unknownv = ?; t = ?
From equation (7.12) we have
v2
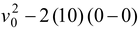
Thus, v ± v 0. At the single point yv 0 −v 0
(d) To find the displacement, Δyy 2 −y 1 , we need equation (7.11);
y 1 −
y 2 −
Hence Δy
(e) Given: y = 15 m; y0 = 0; v0 = 20 m/s
Unknown: t = ?
Since equations (7.9), (7.10) and (7.12) also contain the other unknown, we use equation (7.11)
15 = 0 + 20t−t2
The solutions of the quadratic equations are
t =
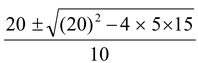
Example 7.9
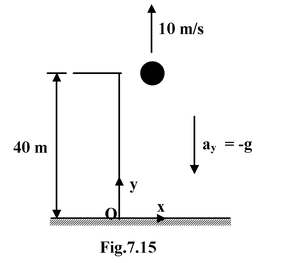
A ball is thrown upward with an initial velocity of 10 m/s from a rooftop 40 m high. Find
(a) its velocity on hitting the ground.
(b) the time of flight
(c) the maximum height
(d) the time to return to roof level
(e) the time it is 15 m below the rooftop.
Solution
|
The origin is assumed at the ground level so that all positions are positive Given: y 0 v 0 a = −10 m/s 2 (a)When the ball lands, its final position coordinate is y = 0 The final velocity v appears as the only unknown in equation (7.12) v 2 2−10) (0−40) = 900 m 2 /s 2 or v = −30 m/s (b) Since v(7.9) |
|
−30 = 10 −t
which gives t = 4 s. If v were unknown we could use equation (7.11)
0 = 40 +10t−t2
(c) At the maximum height v = 0, so from equation (7.12)
0 = (10) 2 −10) (y−
Thus y
(d) At the roof level, the final position is y(7.11)
40 = 40 + 10t−t 2
Therefore, tt
(e) Again from equation (7.11), with y
25 = 40 + 10t−t 2
After solving, we get t
Example 7.10
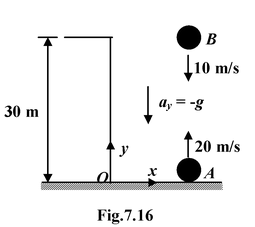
Two balls are thrown towards each other, ball A at 20 m/s upward from the ground, and two second later ball B at 10 m/s downward from a roof 30 m high.
(a) Where and when do they meet
(b) What are their velocities on impact?
Solution
|
Remember in this kind of problem we have to find when before where. We need to write the general expression for the position coordinates. The coordinate system is shown in figure. (a) Given : y0A= 0; v0A= +20 m/s y0B= 30 m; v0B= −10 m/s; a = −10 m/s2. If A has been in motion for time t, then B has been in motion for time (t−(7.11), yA= 20t−t 2 yB= 30 −t−2) −5(t−2) 2 |
|
They meet when yA= yB. This condition immediately leads to t = 3 s. Substituting into either yAor By = 15 m
(b) Since t = 3 s, we have vA= 20 + (−10) (3) = −10 m/s
and vB= −10 + (−10) (3−2) =−20 m/s. Notice that A is already moving downward when it collides with B.
Also Check

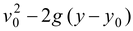 (7.12)
(7.12)