Polynomials

An algebraic expression f(x) of the form f(x) = a₀ + a₁x + a₂x² + ......+ anxn, where a₀, a₁, a₂.......an are real numbers and all the index of x are non-negative integers is called polynomials in x and the highest Index n in called the degree of the polynomial, if

a_n ≠ 0.

DEGREE OF A POLYNOMIAL:

Zero Degree Polynomial:

Any non-zero number is regarded as a polynomial of degree zero or zero degree polynomial. For example, f(x) = a, where a ≠ 0 is a zero degree polynomial, since we can write f(x) = a as f(x) = ax0.

(b) Constant Polynomial:

A polynomial of degree zero is called a constant polynomial. e.g. f(x) = 7.

(c) Linear Polynomial:

A polynomial of degree 1 is called a linear polynomial.

e.g. p(x) = 4x - 3 and f(t) =  √3t + 5 are linear polynomials.

(d) Quadratic Polynomial:

A polynomial of degree 2 is called quadratic polynomial.

e.g. f(x) = 2x2 + 5x –3/5  and g(y) = 3y2 – 5 are quadratic polynomials with real coefficients.

VALUE OF A POLYNOMIAL:

If f(x) is a polynomial and α is any real number, then the real number obtained by replacing x by α in f(x) is called the value of f(x) at x = α and is denoted by f(α).

e.g. Value of p(x) = 5x² - 3x + 7at x = 1 will be

∴ p(1) = 5(1)² - 3(1) + 7

= 5 - 3 + 7 = 9

ZEROS OF A POLYNOMIAL:

A real number α is a zero of polynomial f(x) if f(α) = 0.

The zero of a linear polynomial ax + b is -b/a . i.e.

Geometrically zero of a polynomial is the point where the graph of the function cuts or touches x-axis.

When the graph of the polynomial does not meet the x-axis at all, the polynomial has no real zero.

GRAPH OF POLYNOMIALS:

In algebraic or in set theoretic language the graph of a polynomial f(x) is the collection (or set) of all points (x, y), where y = f(x). In geometrical or in graphical language the graph of a polynomial f(x) is a smooth free hand curve passing through points x₁, y₁), (x₂, y₂), (x₃, y₃), ..... etc. where y₁, y₂, y₃,.... are the values of the polynomial f(x) at x₁, x₂, x₃,.... respectively.

In order to draw the graph of a polynomial f(x), follow the following algorithm.

ALGORITHM:

Step I: Find the values y₁, y_2, ...... yn of polynomial f(x) on different points x₁, x₂, ....... xn………… and prepare a table that gives values of y or  f(x) for various values of x.

Step II: Plot that points (x₁, y₁), (x₂, y₂), (x₃, y₃),.....(x_n, y_n).... on rectangular co-ordinate system. In plotting these points use different scales on the X and Y axes.

Step III: Draw a free hand smooth curve passing through points plotted in step 2 to get the graph of the polynomial f(x).

Graph of a Linear Polynomial:

Consider a linear polynomial f(x) = ax + b, a ≠ 0 Graph of y = ax + b is a straight line. That in why f(x) = ax + b) is called a linear polynomial. Since two points determine a straight line, so only two points need to plotted to draw the line y = ax + b. The line represented by y = ax + b crosses the X-axis at exactly one point, namely.

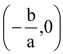1. Draw the graph of the polynomial f(x) = 2x - 5. Also, find the coordinates of the point where it crosses X-axis.

Sol. Let y = 2x - 5.

The following table list the values of y corresponding to different values of  x.

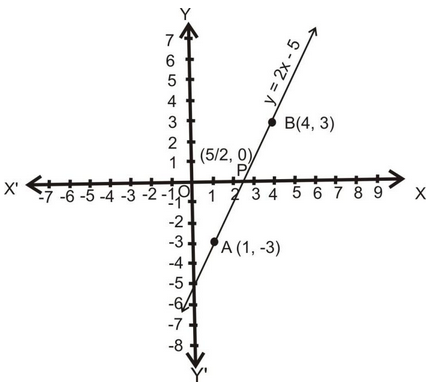
The points A (1, - 3) and B (4, 3) are plotted on the graph paper on a suitable scale. A line is drawn passing through these points to obtain the graphs of the given polynomial.

(b) Graph of a Quadratic Polynomial :

Let a,b,c be real numbers and a ≠ 0. Then f(x) = ax2 + bx + c is known as a quadratic polynomial in x. Graph of the quadratic polynomial i.e. he curve whose equation is y = ax2 + bx + c, a ≠ 0 Graph of a quadratic polynomial is always a parabola.

Let y = ax² + bx + c, where a ≠ 0

⇒ 4ay = 4a²x² + 4abx + 4ac

⇒ 4ay = 4a²x² + 4abx + b² – b² + 4ac

⇒ 4ay = (2ax + b)² – (b² - 4ac)

⇒ 4ay + (b2 – 4ac) = (2ax + b)² ⇒ 4ay + (b² – 4ac) = 4a² (x + b/2a)²

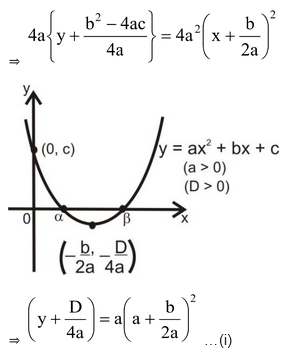
where D = b² - 4ac is the discriminate of the quadratic equation.

Remarks:

Shifting the origin at 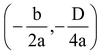, we have X = x - 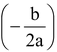and Y = y -

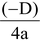
Substituting these values in (i), we obtain

Y = aX² ....(ii)

which is the standard equation of parabola

Clearly, this is the equation of a parabola having its vertex at .

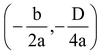The parabola opens upwards or downwards according as a > 0 or a < 0.

SIGNS OF COEFFICIENTS OF A QUADRATIC POLYNOMIAL:

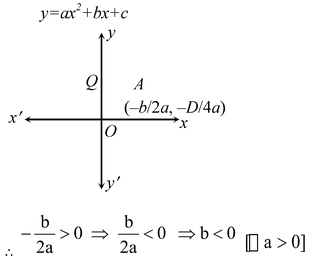
The graphs of y = ax² + bx + c are given in figure. Identify the signs of a, b and c in each of the following:

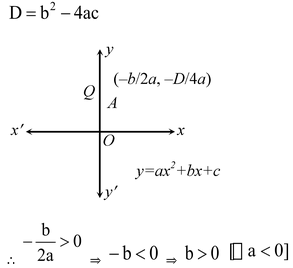
(i) We observe that y = ax² + bx + c represents a parabola opening downwards. Therefore, a < 0. We observe that the turning point 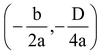of the parabola is in first quadrant where

Parabola y = ax² + bx + c cuts y-axis at Q. On y-axis, we have x = 0.

Putting x = 0 in y = ax² + bx + c we get y = c.

So, the coordinates of Q are (0, c). As Q lies on the positive direction of y-axis. Therefore, c > 0.

Hence, a < 0, b > 0 and c > 0.

(ii) We find that y = ax² + bx + c represents a parabola opening upwards. Therefore, a > 0 The turning point of the parabola is in fourth quadrant.

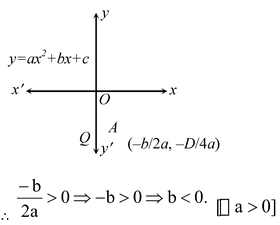
Parabola y = ax² + bx + c cuts y-axis at Q and y-axis. We have x = 0. Therefore, on putting x = 0 in y = ax² + bx + c we get y = c.

So, the coordinates of Q are (0, c). As Q lies on negative y-axis. Therefore, c < 0.

Hence, a > 0, b < 0 and c < 0.

(iii) Clearly, y = ax² + bx + c represents a parabola opening upwards.

Therefore, a > 0. The turning point of the parabola lies on positive direction of x-axis.

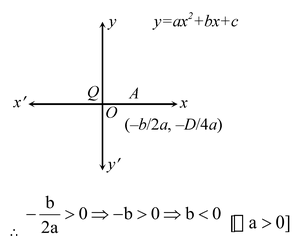
The parabola y = ax² + bx + c cuts y-axis at Q which lies on positive y-axis. Putting
x = 0 in y = ax² + bx + c we get y = c. So, the coordinates of Q are (0, c). Clearly, Q lies on OY.

∴ c > 0.

Hence, a > 0, b < 0, and c > 0.

(iv) The parabola y = ax² + bx + c opens downwards. Therefore, a < 0.

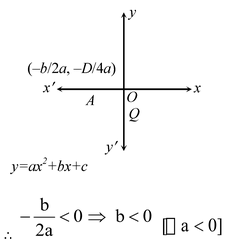
The turning point 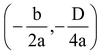of the parabola is on negative x-axis,

Parabola y = ax² + bx + c cuts y-axis at Q (0, c) which lies on negative y-axis. Therefore, c < 0.

Hence,  a < 0, b < 0and c < 0.

(v) We notice that the parabola y = ax² + bx + c opens upwards. Therefore, a > 0.

Turning point 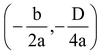of the parabola lies in the first quadrant.

As Q (0, c) lies on positive y-axis. Therefore, c > 0.

Hence, a >0, b < 0 and c > 0.

(vi) Clearly, a < 0

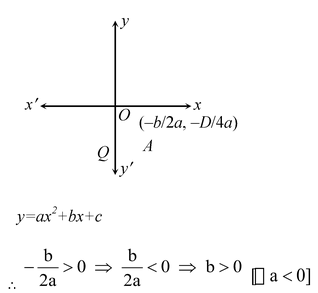
Turning point 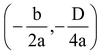of the parabola lies in the fourth quadrant.

As Q (0, c) lies on negative y-axis. Therefore, c < 0.

Hence,  a < 0, b> 0 and c < 0.