
How To Draw Graph Of Quadratic Polynomials
Polynomials of Class 10
A quadratic polynomial graph is a parabola. The roots of the quadratic figure are points where the parabola cuts the x axis i.e. points where the quadratic polynomial value is zero. There are certain steps you need to follow while making graph for quadratic polynomials:
Write the given quadratic polynomial f(x)= ax 2 + bx+ c as Y = ax 2 + bx + c
Calculate the zeros of the polynomial, if exist, by putting y = 0 i.e., ax 2 + bx + c
Calculate the points where the curve meets y-axis by putting x = 0.
Calculate D = b 2 – 4ac
if D > 0, graph cuts x-axis at two points.
D = 0, graph touches x-axis at one point.
D < 0, graph is far away from x-axis.
Find
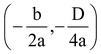 which is the turning point of curve.
which is the turning point of curve.
Make a table of selecting values of x and corresponding values of y, two to three values on left and two to three values on right of turning point
Draw a smooth curve through these points by free hand. The graph so obtained is called a parabola.
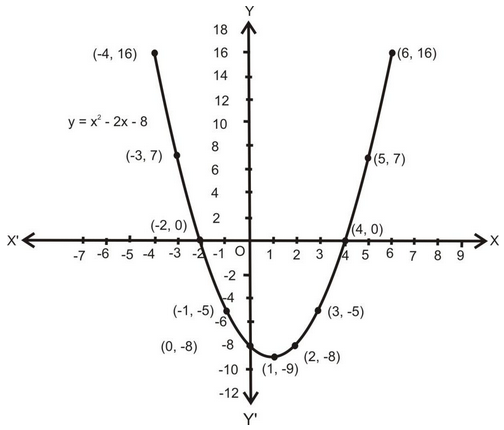
Q1. Draw the graph of the polynomial f(x) = x 2 – 2x – 8
Sol. Let y = x 2 - 2x - 8.
The following table gives the values of y or f(x) for various values of x.
|
x |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
y = x 2 – 2x - 8 |
16 |
7 |
0 |
-5 |
-8 |
-9 |
-8 |
-5 |
0 |
7 |
16 |
Let us plot the points (-4, 16), (-3, 7), (-2, 0), (-1, -5), (0, - 8), (1, - 9), (2, - 8), (3, - 5), (4, 0), (5, 7) and (6, 16) on a graphs paper and draw a smooth free hand curve passing through these points. The curve thus obtained represents the graphs of the polynomial f(x) = x2 - 2x - 8. This is called a parabola.
The lowest point P, called a minimum point, is the vertex of the parabola. Vertical line passing through P is called the axis of the parabola. Parabola is symmetric about the axis. So, it is also called the line of symmetry.
Observations:
For the graphs of the polynomial f(x) = x 2 - 2x - 8, following observations can be drawn:
- The coefficient of x2 in f(x) = x 2 - 2x - 8 is 1 (a positive real number) and so the parabola opens upwards.
- D = b 2 - 4ac = 4 + 32 = 36 > 0. So, the parabola cuts X-axis at two distinct points.
- On comparing the polynomial x 2 - 2x - 8 with ax 2 + bx + c, we get a = 1, b = –2 and c = –8.
The vertex of the parabola has coordinates (1, -9) i.e.
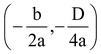 , where D ≡ b2 - 4ac.
, where D ≡ b2 - 4ac.
- The polynomial f(x) = x 2 – 2x – 8 = (x – 4) (x + 2) is factorizable into two distinct linear factors (x – 4) and (x + 2). So, the parabola cuts X-axis at two distinct points (4, 0) and (–2, 0). The x-coordinates of these points are zeros of f(x).
For additional information related to the subject you can check the Maths Formula section.
Graph of a Cubic Polynomial
Graphs of a cubic polynomial does not have a fixed standard shape. Cubic polynomial graphs will always cross X-axis at least once and at most thrice.
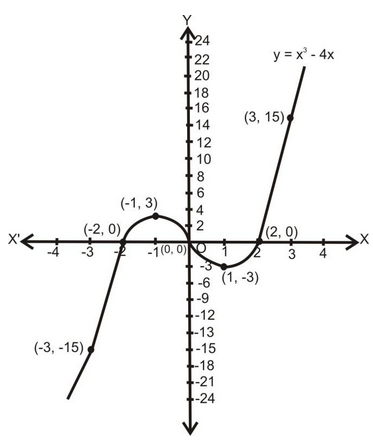
Q1. Draw the graphs of the polynomial f(x) = x 3 - 4x.
Sol. Let y = f(x) or, y = x 2 – 4x.
The values of y for variable value of x are listed in the following table :
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
|
y = x 3 – 4x |
–15 |
0 |
3 |
0 |
–3 |
0 |
15 |
Thus, the curve y = x 3 – 4x passes through the points (–3, –15), (–2, 0), (–1, 3), (0 ,0), (1, –3), (2, 0), (3, 15), (4, 48) etc.
Plotting these points on a graph paper and drawing a free hand smooth curve through these points, we obtain the graph of the given polynomial as shown figure.
Observations:
For the graphs of the polynomial f(x) = x 3 – 4x, following observations are as follows:
- The polynomial f(x) = x 3 - 4x = x(x 2 – 4) = x(x – 2) (x + 2) is factorizable into three distinct linear factors. The curve y = f(x) also cuts X-axis at three distinct points.
- We have, f(x) = x (x – 2) (x + 2). Therefore 0, 2 and -2 are three zeros of f(x). The curve y = f(x) cuts X-axis at three points O (0, 0), P(2, 0) and Q (-2, 0).
Relationship Between Zeros and Coefficient of a Quadratic Polynomial
Let α and β be the zeros of a quadratic polynomial f(x) = ax2 + bx + c. By facto r theorem ( x - α) and (x - β) are the factors of f(x).
∴ f(x) = k ( x - α) (x - β) are the factors of f(x)
⇒ ax 2 + bx + c = k{x 2 - (α + β)x + αβ}
⇒ ax 2 + bx + c = kx 2 - k(α + β)x + kαβ
Comparing the coefficients of x 2 , x and constant terms on both sides, we get a = k, b = –k (α+ β) and kαβ
⇒
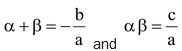
⇒
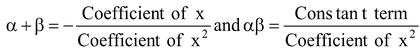
Hence,
Sum of the zeros
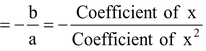
Product of the zeros

REMARKS:
If α and β are the zeros of a quadratic polynomial f(x). The , the polynomial f(x) is given by
f(x) = k{x 2 - (α + β)x + αβ}
or f(x) = k{x 2 - (Sum of the zeros) x + Product of the zeros}
Q1. Find a quadratic polynomial whose zeros are 5 +√2 and 5 - √2.
Sol. Given α = 5 +√2, β = 5 - √2
∴ f(x) = k{x 2 - (α + β)x + αβ}
Here,
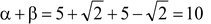
and
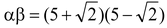
= 25 – 2 = 23
∴ f(x) = k {x 2 – 10x + 23}, where, k is any non-zero real number.
Relationship Between Zeros and Coefficient of a Cubic Polynomial
Let α,β,γ be the zeros of a cubic polynomial f(x) = ax 3 + bx 2 + cx + d, a ≠ 0 Then, by factor theorem,(x - α), (x - β) and (x - γ) are factors of f(x). Also, f(x) being a cubic polynomial cannot have more than three linear factors.
∴ f(x) = k (x - α)(x - β) (x - γ)
⇒ ax 3 + bx 2 + cx + d = k (x - α)(x - β) (x - γ)
⇒ ax
3
+ bx
2
+ cx + d = k{x
3
–
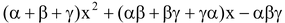 }
}
⇒ ax
3
+ bx
2
+ cx + d = k x
3
- k
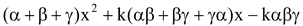
Comparing the coefficients of x 3 , x 2 , x and constant terms on both sides, we get
a = k, b = –k
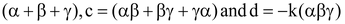
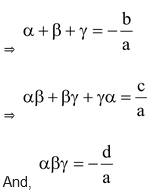
⇒ Sum of the zeros
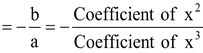
⇒ Sum of the products of the zeros taken two at a time
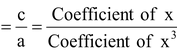
⇒ Product of the zeros
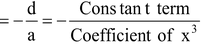
Remarks :
Cubic polynomial having α,β and γ as its zeros is given by
∴ f(x) = k (x - α)(x - β) (x - γ)
f(x) = k {x
3
-
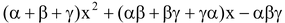 } where k is any non-zero real number.
} where k is any non-zero real number.
Q1. Form a cubic polynomial with zeros α = 3, β = 2, γ = –1 .
Sol. α = 3, β = 2, γ = –1
Required polynomial = k (x - α)(x - β) (x - γ)
= k[(x - 3) (x - 2) (x + 1)]
= k[(x 2 - 5x + 6)(x + 1)]
= k[x 3 - 5x 2 + 6x + x 2 - 5x + 6]
= k[x 3 - 4x 2 + x + 6]
where k is a non-zero constant.
Students can also access the class 10 Math Notes from here.
Also Check









