Methods Of Solving Quadratic Equation

BY FACTORISATION:

Algorithm:

question 1. Solve the following quadratic equation by factorisation method: x² – 2ax + a² – b² = 0.

Solution: Here, Factors of constant term (a² – b²) are (a – b) and (a + b).

Also, Coefficient of the middle term = –2a = –[(a – b) + (a + b)]

∴ x² – 2ax + a² – b² = 0

⇒ x² – {(a – b) + (a + b)}x + (a – b)(a + b) = 0

⇒ x² – (a – b) x – (a + b) x + (a – b) (a + b) = 0

⇒ x{x – (a – b)} – (a + b) {x – (a – b)} = 0

⇒ {x – (a – b)} {x – (a + b)} = 0

⇒ x – (a – b) = 0 or, x – (a + b) = 0

⇒ x = a - b or x = a + b

question 2. Solve 64x² - 625 = 0

Solution: We have 64x² – 625 = 0

or (8x)² – (25)² = 0

or (8x + 25) (8x – 25) = 0

i.e. 8x + 25 = 0 o 8x – 25 = 0.

This gives x = 25/8 or 25/8

Thus, x = - 25/8, 25/8 are solutions of the given equations.

BY THE METHOD OF COMPLETION OF SQUARE:

Algorithm:

Step-(i) Obtain the quadratic equation. Let the quadratic equation be ax² + bx + c = 0, a ≠ 0.

Step-(ii) Make the coefficient of x² unity, if it is not unity. i.e., obtained

Step-(iii) Shift the constant term c/a  on R.H.S. to get x2 +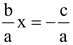

Step-(iv) Add square of half of the coefficient of x i.e. 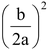on both sides to obtain

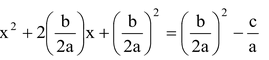
Step-(v) Write L.H.S. as the perfect square of a binomial expression and simplify R.H.S. to get

.

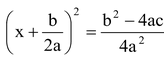Step-(vi) Take square root of both sides to get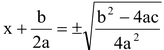

Step (vii) Obtain the values of x by shifting the constant term b/2a on RHS.

question 1. Solve :- x² + 3x + 1 = 0

Solution: We have

x² + 3x + 1 = 0

Add and subtract (1/2 coefficient of x)² in L.H.S. and get

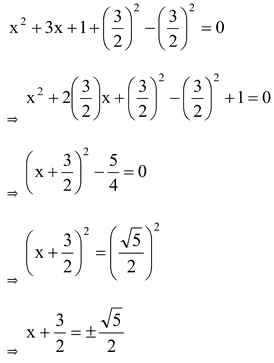
This gives

Therefore are the solutions of the given equation.

BY USING QUADRATIC FORMULA:

Solve the quadratic equation in general form viz. ax² + bx + c = 0.

We have, ax² + bx + c = 0

Step (i) By comparison with general quadratic equation, find the value of a,b and c.

Step (ii) Find the discriminant of the quadratic equation.

D = b² – 4ac

Step (iii) Now find the roots of the equation by given equation

REMARK:

If b² - 4ac < 0 i.e. negative, then is not real and therefore, the equation does not have any real roots.

question 1. Solve the quadratic equation x² – 7x – 5 = 0.

Solution: Comparing the given equation with ax² + bx + c = 0, we find that a = 1, b = –7 and c = –5.

Therefore, D = (–7)² - 4 × 1 × (–5) = 49 + 20 = 69 > 0

Since D is positive, the equation has two roots given by

⇒ x = are the required solutions.

question 2. For what value of k, (4 – k)x² + (2k + 4)x + (8k + 1) is a perfect square.

Solution: The given equation is a perfect square, if its discriminant is zero i.e. (2k + 4)² – 4(4 - k) (8k + 1) = 0

⇒ 4(k + 2)² – 4(4 – k) (8k + 1) = 0 ⇒ 4[4(k + 2)² – (4 – k) (8k + 1)] = 0

⇒ [(k² + 4k + 4) – (–8k² + 31k + 4)] = 0 ⇒ 9k² – 27k = 0

⇒ 9k (k – 3) = 0 ⇒ k = 0 or k = 3

Hence, the given equation is a perfect square, if k = 0 or k = 3.