NCERT Solution for class 8 maths chapter -10 Visualising Solid Shapes

The NCERT solutions for class 8 maths chapter 10 Visualising Solid Shapes is prepared by academic team of Physics Wallah . We have prepared solutions for all exercise of chapter 10. Given below is step by step NCERT solutions of all questions given in NCERT textbook for chapter 10. Read chapter 10 theory make sure you have gone through the theory part of chapter 10 from NCERT textbook and you have learned the formula of the given chapter. Physics Wallah prepared a detail notes and additional importants questions for class 8 maths with short notes of all maths formula of class 8 maths. Do read these contents before moving to solve the exercise of NCERT chapter 10.

NCERT Solutions for Class 8 Maths Exercise 10.1

Question 1.

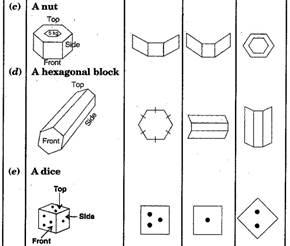
For each of the given solid, the two views are given. Match for each solid the corresponding top and front views. The first one is done for you.

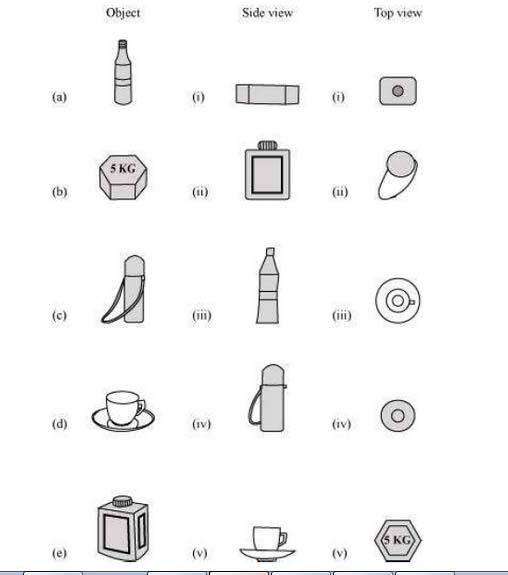
Solution :

(a) (iii); (iv)
(b); (i); ; (v)
(c); (iv) (ii)
(d) (v); (iii)
(e) (ii); (i)
;

Question 2.

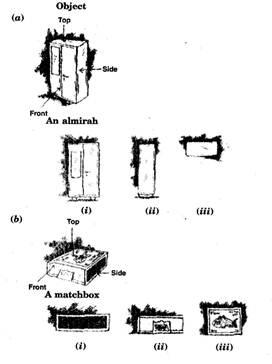
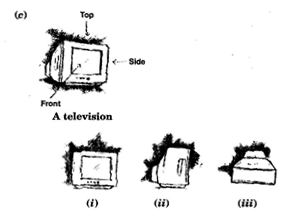
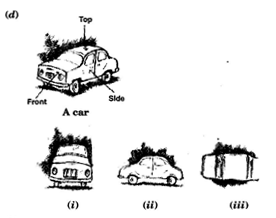
For each of the given solid, the three views are given. Identify for each solid the corresponding top, front and side views.
;

Solution :

(a);(i); Front
(ii) Side
(iii) Top view
(b) (i); Side
(ii) Front
(iii); Top view
(c) (i); Front
(ii); Side
(iii) Top view
(d) (i); Front
(ii); Side
(iii); Top view

Question 3.

For each given solid, identify the top view, front view and side view.

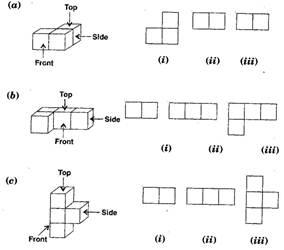
Solution :

(a); (i) Top view (ii); Front view (iii); Side view
(b) (i) Side view (ii) Front view (iii); Top view
(c); (i); Top view (ii); Side view (iii) Front view
(d); (i) Side view (ii) Front view (iii) Top view
(e) (i); Front view (ii); Top view (iii) Side view

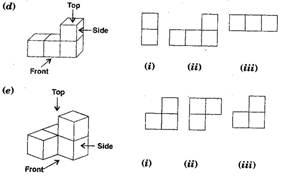
Question 4.

Draw the front view, side view and top view of the given objects:

Solution :

 

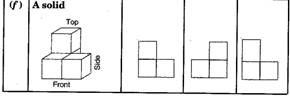
NCERT Solutions for Class 8 Maths Exercise 10.2

 

Question 1.

Can a polygon have for its faces:
(i) 3 triangles ;
(ii) 4 triangles
(iii) a square and four triangles

Solution :

(i) No, a polyhedron cannot have 3 triangles for its faces.
(ii) Yes, a polyhedron can have four triangles which is known as pyramid on triangular base.
(iii) Yes, a polyhedron has its faces a square and four triangles which makes a pyramid on square base.

Question 2.

Is it possible to have a polyhedron with any given number of faces? (Hint: Think of a pyramid)

Ans.

It is possible, only if the number of faces are greater than or equal to 4.

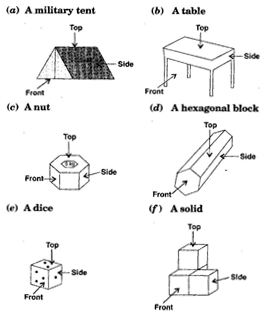
Question 3.

Which are prisms among the following:

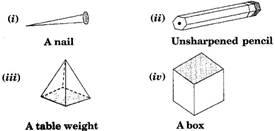
Solution :

Figure (ii) unsharpened pencil and figure (iv) a box are prisms.

Question 4.

(i) How are prisms and cylinders alike?
(ii) How are pyramids and cones alike?

Solution :

(i) A prism becomes a cylinder as the number of sides of its base becomes larger and larger.
(ii) A pyramid becomes a cone as the number of sides of its base becomes larger and larger.

Question 5.

Is a square prism same as a cube? Explain.

Solution :

No, it can be a cuboid also.

Question 6.

Verify Euler’s formula for these solids.

Solution :

(i) Here, figure (i) contains 7 faces, 10 vertices and 15 edges.
Using Eucler’s formula, we see
F + V – E = 2
Putting F = 7, V = 10 and E = 15,
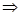F + V – E = 2
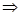7 + 10 – 5 = 2
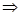17 – 15 = 2
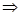2 = 2
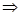L.H.S. = R.H.S.
(ii); Here, figure (ii) contains 9 faces, 9 vertices and 16 edges.
Using Eucler’s formula, we see
F + V – E = 2
F + V – E = 2
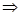9 + 9 – 16 = 2
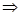18 – 16 = 2
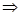2 = 2
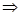L.H.S. = R.H.S.
Hence verified Eucler’s formula.

Question 7.

Using Euler’s formula, find the unknown:

Solution :

In first column, F = ?, V = 6 and
E = 12
Using Eucler’s formula, we see
F + V – E = 2
F + V – E = 2
;F + 6 – 12 = 2
;F – 6 = 2
;F = 2 + 6 = 8
Hence there are 8 faces.
In second column, F = 5, V = ? and E = 9
Using Eucler’s formula, we see
F + V – E = 2
F + V – E = 2
;5 + V – 9 = 2
;V – 4 = 2
;V = 2 + 4 = 6
Hence there are 6 vertices.
In third column, F = 20, V = 12 and E = ?
Using Eucler’s formula, we see
F + V – E = 2
F + V – E = 2
;20 + 12 – E = 2
;32 – E = 2
;E = 32 – 2 = 30
 Hence there are 30 edges.

Question 8.

Can a polyhedron have 10 faces, 20 edges and 15 vertices?

Solution :

If F = 10, V = 15 and E = 20.
Then, we know Using Eucler’s formula,
F + V – E = 2
L.H.S. = F + V – E
= 10 + 15 – 20
= 25 – 20
= 5
R.H.S.; = 2
 Hence  L.H.S. R.H.S.
Therefore, it does not follow Eucler’s formula.
So polyhedron cannot have 10 faces, 20 edges and 15 vertices.

 

NCERT Solutions for Class 8 Maths Exercise 10.3

 

 

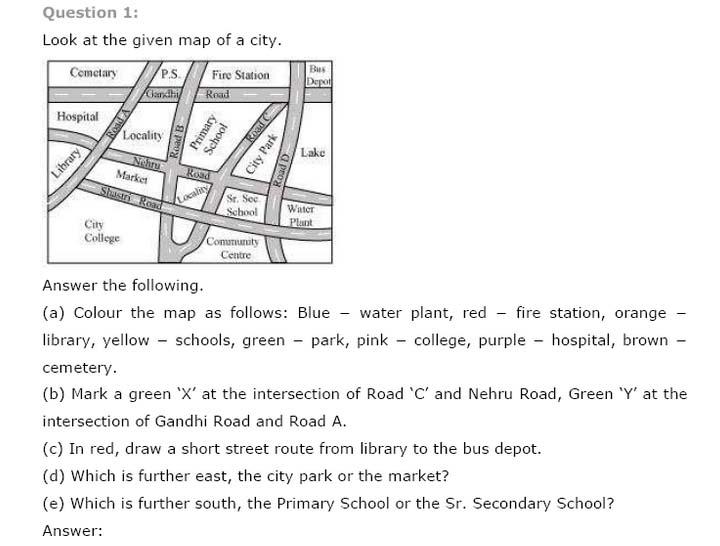
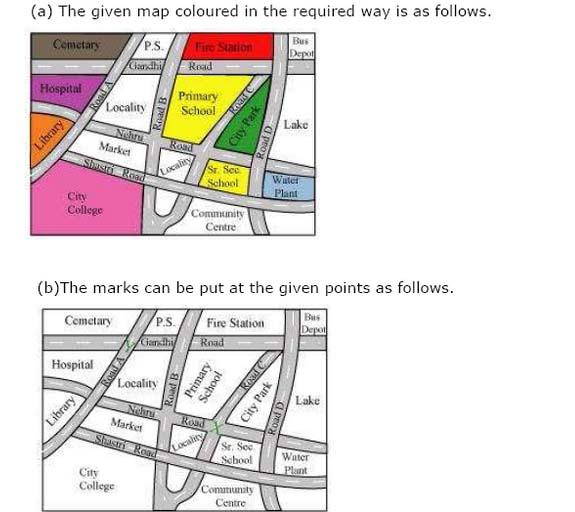
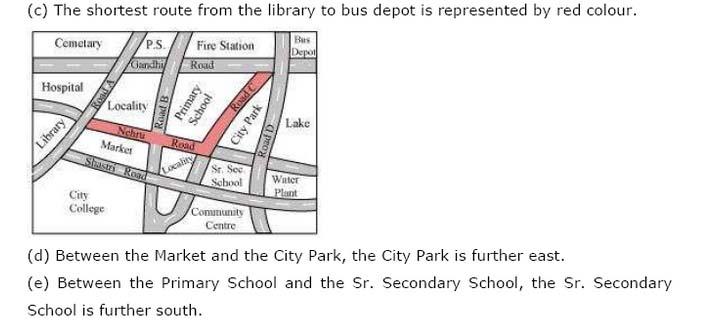
Notes,worksheet and solved question for Maths class 8

 

1. ;class 8 maths notes on chapter Liner equation in one variable
2. class 8 maths notes on chapter algebric expression
3. class 8 maths notes on chapter Mensuration;
4. class 8 maths notes on chapter Square and square roots
5. class 8 maths notes on chapter statistice
6. class 8 maths notes on chapter practical Geometry
7. class 8 maths notes on chapter commericial maths
8. class 8 maths notes on chapter solid shape
9. class 8 maths notes on chapter quadrilaterals
10. class 8 maths notes on chapter exponents
11. class 8 maths notes on chapter factorisation;
12. class 8 maths notes on chapter inverse proporation
13. class 8 maths notes on chapter cube and cube roots

Check your marks in a chapter which you have complited in school from Physics Wallah chapter wise online test just click on the link given below

chapter wise online test for class 8 maths