
NCERT Solution for class chapter-16 Playing with Numbers
NCERT solutions for class 8 maths chapter 16 Playing with Numbers is prepared by academic team of Physics Wallah. We have prepared solutions for all exercise of chapter 16 . Given below is step by step solutions of all questions given in NCERT textbook for chapter 16. Read chapter 16 theory make sure you have gone through the theory part of chapter 16 from NCERT textbook and you have learned the formula of the given chapter. Physics Wallah prepared a detail notes and additional questions for class 8 maths with short notes of all maths formula of class 8 maths. do read these contents before moving to solve the exercise of NCERT chapter 16. This NCERT solution contains questions, answers, pictures and explanations for the complete Chapter 16.
NCERT Solutions for Class 8 Maths Exercise 16.1
Find the values of the letters in each of the following and give reasons for the steps involved.
Question 1.
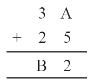
Solution :
On putting A = 1, 2, 3, 4, 5, 6, 7 and so on and we get, 7 + 5 = 12 in which ones place is 2.
∴ A = 7
And putting 2 and carry over 1, we get
B = 6
Hence A = 7 and B = 6
Question 2.
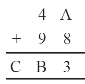
Solution :
On putting A = 1, 2, 3, 4, 5, 6, 7 and so on and we get,8 + 5 = 13 in which ones place is 3.
∴ A = 5
And putting 3 and carry over 1, we get
B = 4 and C = 1
Hence A = 5, B = 4 and C = 1
Question 3.
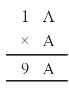
Solution :
On putting A = 1, 2, 3, 4, 5, 6, 7 and so on and we get, A x A = 6 x 6 = 36 in which ones place is 6.
∴ A = 6
Hence A = 6
Question 4.
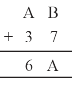
Solution :
Here, we observe that B = 5
so that 7 + 5 = 12.
Putting 2 at ones place and carry over 1 and A = 2, we get
2 + 3 + 1 = 6
Hence A = 2 and B = 5
Question 5.
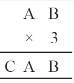
Solution :
Here on putting B = 0,
we get 0 × 3 = 0.
And A = 5, then 5 × 3 = 15
⇒ A = 5 and C = 1
Hence A = 5, B = 0 and C = 1
Question 6.
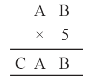
Solution :
On putting B = 0, we get 0 , 5 = 0 and A = 5, then 5×5 = 25
⇒ A = 5, C = 2
Hence A = 5, B = 0 and C = 2
Question 7.
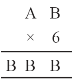
Solution :
Here product of B and 6 must be same as ones place digit as B.
6 ×1 = 6, 6 ×2 = 12, 6 ×3 = 18,
6 ×4 = 24
On putting B = 4, we get the ones digit 4 and remaining two B’s value should be 44.
∴ For 6 × 7 = 42 + 2 = 44
Hence A = 7 and B = 4
Question 8.
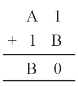
Solution :
On putting B = 9, we get 9 + 1 = 10
Putting 0 at ones place and carry over 1, we get
For A = 7 ⇒ 7 + 1 + 1 = 9
Hence A = 7 and B = 9
Question 9.
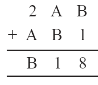
Solution :
On putting B = 7,
⇒ 7 + 1 = 8
Now A = 4, then 4 + 7 = 11
Putting 1 at tens place and carry over 1, we get
2 + 4 + 1 = 7
Hence A = 4 and B = 7
Question 10.
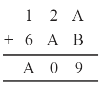
Solution :
Putting A = 8 and B = 1, we get
8 + 1 = 9
Now again we add 2 + 8 = 10
Tens place digit is ‘0’ and carry over 1.
Now 1 + 6 + 1 = 8 = A
Hence A = 8 and B = 1
NCERT Solutions for Class 8 Maths Exercise 16.1
Question 1.
If 21y 5 is a multiple of 9, where y is a digit, what is the value of y?
Solution :
Since 21y 5 is a multiple of 9.
Therefore according to the divisibility rule of 9, the sum of all the digits should be a multiple of 9.
∴ 2 + 1 y + 5 = 8 +y
⇒ 8 + y = 9
⇒ y = 1
Since 21y5 is a multiple of 9.
Question 2.
If 31z
Solution :
Since 31z5 is a multiple of 9.
Therefore according to the divisibility rule of 9, the sum of all the digits should be a multiple of 9.
∴ 3 + 1 + z + 5 = 9 + z
⇒ 9 + z = 9
⇒ z = 0
If 3 + 1 + z + 5 = 9 + z
⇒ 9 + z = 18
⇒ z = 9
Hence 0 and 9 are two possible answers.
Question 3.
If 24x is a multiple of 3, where x is a digit, what is the value of x?
(Since 24x is a multiple of 3, its sum of digits 6 + x is a multiple of 3; so 6 + x is one of these numbers: 0, 3, 6, 9, 12, 15, 18, … .But since x is a digit, it can only be that
6 + x = 6 or 9 or 12 or 15. Therefore, x = 0 or 3 or 6 or 9. Thus, x can have any of (four different values.)
Solution :
Since 24x is a multiple of 3.
Therefore according to the divisibility rule of 3, the sum of all the digits should be a multiple of 3.
∴ 2 + 4 + x = 6 + x
Since x is a digit.
⇒6 + x = 6 ⇒
![]()
⇒ 6 + x = 9 ⇒
![]()
⇒ 6 + x = 12 ⇒
![]()
⇒ 6 + x = 15 ⇒
![]()
Thus, x can have any of four different values.
Question 4.
If 31z5 is a multiple of 3, where z is a digit, what might be the values of z?
Solution :
Since 31z 5 is a multiple of 3.
Therefore according to the divisibility rule of 3, the sum of all the digits should be a multiple of 3.
Since z is a digit.
∴ 3 + 1 + z + 5 = 9 +z
⇒ 9 +z = 9 ⇒ z = 0
If 3 + 1 + z + 5 = 9 + z
⇒ 9 + z = 12 ⇒ z = 3
If 3 + 1 + z + 5 = 9 + z
⇒ 9 + z = 15 ⇒ z = 6
If 3 + 1 + z + 5 = 9 + z
⇒ 9 + z = 15 ⇒ z = 9
Hence 0, 3, 6 and 9 are four possible answers.
Notes,worksheet and solved question for Maths class 8
- class 8 maths notes on chapter Liner equation in one variable
- class 8 maths notes on chapter algebric expression
- class 8 maths notes on chapter Mensuration
- class 8 maths notes on chapter Square and square roots
- class 8 maths notes on chapter statistice
- class 8 maths notes on chapter practical Geometry
- class 8 maths notes on chapter commericial maths
- class 8 maths notes on chapter solid shape
- class 8 maths notes on chapter quadrilaterals
- class 8 maths notes on chapter exponents
- class 8 maths notes on chapter factorisation
- class 8 maths notes on chapter inverse proporation
- class 8 maths notes on chapter cube and cube roots
Check your marks in a chapter which you have complited in school from Physics Wallah chapter wise online test just click on the link given below
chapter wise online test for class 8 maths









