Relative Velocity In Two Dimensions, River-boat Problems, Important Topics For JEE 2025

Relative Velocity in Two Dimensions : In this section, we describe how observations made by different observers in different frames of reference are related to each other. We find that observers in different frames of reference may measure different positions, velocities, and accelerations for a given particle. That is, two observers moving relative to each other generally do not agree on the outcome of a measurement.

JEE Main Seat Matrix 2024 : Click to Check

IIT Allahabad Seat Matrix : Click To Check

River-boat Problems

While solving problems related to river boat or river swimmer we come across the following terms

(a) Absolute velocity of swimmer/boatman or (absolute means velocity relative to ground)

(b) Absolute velocity of river current and

(c) Velocity of swimmer/boatman with respect to the river v _sr or v _br

Since, v _sr = v _s – v _r

v _s = v _sr + v _r …(1)

Observing the situation shown in the diagram below, we arrive at some standard results and their special cases.

Consider a river of width l across which a swimmer wants to swim. Let V _sr be the relative velocity of swimmer with respect to river current and let V _sr make an angle with PQ shown in the figure. Let us assume the flow of river to be along the positive x -axis.

Since from (1), we get

It t is the time taken by the swimmer to cross the river, then

…(4)

Further if x is the drift (displacement along x axis) when he reached the opposite bank, then

x = ( v b ) x t

…(5)

Since

For t to be MINIMUM, must be MAXIMUM

i.e., = 1

The relative velocity of swimmer with respect to river must be perpendicular to the river current.

As a result of this the swimmer will be drifted to the point B .

So, …(6)

Colleges Accepting JEE Main Score 2024 : Click to Check

Relative Velocity : Condition For Zero Drift  Or Condition To Reach The Opposite Point

Since we calculated the drift value to be x given by

For the above condition to be met, we must have

x = 0

…(7)

A diagrammatic representation is given in support of the above mathematical argument.

Let be the velocity of swimmer relative to river current, the river current, then the swimmer wants to swim in a manner such that he reaches the point just opposite to the point from where he started. For such a thing to happen he must have his relative velocity directed in a direction opposite to the river current at an angle θ to the line PQ (say).

Further since

So,

So, we conclude that the swimmer reached Q when he directs his velocity relative to river at an angle upstream from PQ .

Also we observe that if v r > v sr then the swimmer would never reach the point Q .

JEE Advanced Cutoff 2024 : Click To Check

Relative Velocity : Condition for Minimum Drift

For minimising the drift, we must have

If we are asked to calculated the angle with the horizontal, then we get

Total angle =

Also, we conclude that the drift x can be minimised only if v sr < v r .

JEE Advanced Result  2024 : Click To Check

Aeroplane-wind Problems

These problems proceed the same way as we have done for river-swimmer problems or river-boat problems. Here is just replaced by (velocity of aircraft with respect to wind), where

JEE Question Banks : Click to Check

Let us understand with the help of an Example

Ex. A plane moves in windy weather due east while the pilot points the plane somewhat south of east. The wind is blowing at 50 km/hr directed 30° east of north, while the plane moves at 200 km/hr relative to the wind. What is the velocity of the plane relative to the ground and what is the direction in which the pilot points the plane?

Ans. Three vectors are involved. We have to find the magnitude of and the direction of (i.e., ). Let us first relate the three vectors using the concept of relative velocity. We can write

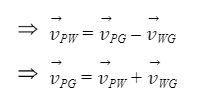
Here we have two unknown quantities (V _PG and θ), so we should not relate the magnitudes of these vectors using triangle law. In such situations we resolve the vectors into components on the coordinate system and then solve the equations for both axes ( x and y ).

For the y components

v PG , y = v PW, y + v WG, y

i.e., 0 = –(200) sin θ + (50 cos 30°)

Solving, we get

For the x components

v PG , x = v PW, x + v WG, x

v PG = (200 cos θ) + (50 sin 30°)

v PG = 221 km/h –1

JEE Main Previous Year Paper : Click to Check

Rain -man Problems

In such problems we come across the following terminology according to which

(a) is the absolute velocity of rain.

(b) is the absolute velocity of man/cyclist/ motorist/observer.

(c) is the absolute velocity of wind (if it is blowing) and

(d) is the velocity of rain with respect to man or the velocity of rain which appears to the man.

For dealing with such like problems, we have two options

Option A:

When no wind is blowing.

v _rm = v _r – v _m or v _rm = v _r + (– v _m )

So, while dealing with the problems in which rain and man are there but no wind exists, then to calculate the direction of v _rm , we simply reverse the direction of man's velocity (– v _m ) and then find the resultant of – v _m and v _r i.e., – v _r + (– v _m ) to get the direction and magnitude of v _rm . It's the Best Trick! Try following and see the results.

Option B:

When wind is blowing.

v _rm = ( v _r + v _w ) – v _m or v _rm = v _r + v _w + (– v _m )

So, while dealing with the problems involving rain, man and the blowing wind we first calculate the resultant of rain and wind i.e., net velocity of rain under the inference of wind v _r + v _w = v _{net rain} – v _m . The man sees this rain falling with a velocity v _rm = v _{net rain} – v _m

v _rm = ( v _r + v _w ) – v _m

v _rm = ( v _r + v _w ) + (– v _m )

Again, we reverse the direction of velocity of man and then find the resultant of v _{net rain} and – v _m to get v _rm with magnitude and direction.

So, to deal with problems involving rain, man and wind we just reverse the direction of v _m i.e., make it – v _m and then find the resultant of v _r , v _w and – v _m i.e., v _r + v _w + (– v _m )