Circle
Area Related To Circles of Class 10
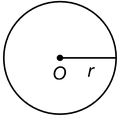
The set of points which are at a constant distance of units from a fixed point O is called a circle with centre O and radius = r units. The circle is denoted by C(O, r).
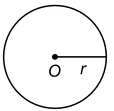
The fixed point O is called the centre and the constant distance r units is called its radius.
Results:
(i) If two circles touch internally, then the distance between their centers is equal to the difference of their radii.
(ii) If two circles touch externally, then the distance between their centers is equal to the sum of their radii.
(iii) Distance moved by a rotating wheel in one revolution is equal to the circumference of the wheel.
(iv) Number of revolutions completed by a rotating wheel in one minute:

(v) Angle described by minute hand in one minute = 6o.
(vi) Angle described by hour hand in one hour = 30o.
CIRCUMFERENCE:
The perimeter (or length of boundary) of a circle is called its circumference.
ARC:
A continuous piece of a circle is called an arc of the circle.
In the given figure, PQ is an arc of a circle, with centre O, denoted by
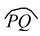 . The remaining part of the circle, represents
. The remaining part of the circle, represents
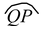 .
.
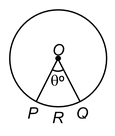
CENTRAL ANGLE:
An angle subtended by an arc at the centre of a circle is called its central angle.
In the given figure of a circle with centre O, central angle of
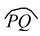 = ∠POQ = θº.
= ∠POQ = θº.
If θº < 180º then the arc
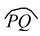 is called the minor arc and the arc
is called the minor arc and the arc
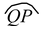 is called the major arc.
is called the major arc.
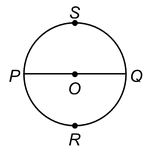
SEMICIRCLE:
A diameter divides a circle into two equal arcs. Each of these two arcs is called a semicircle.
In the given figure of a circle with centre O,
 and
and
 are semicircles.
are semicircles.
An arc whose length is less than the arc of a semicircle is called a minor arc. An arc whose length is more than the arc of a semicircle is called a major arc.
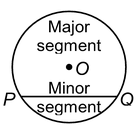
SEGMENT:
A segment of a circle is the region bounded by an arc and a chord, including the arc and the chord.
The segment containing the minor arc is called a minor segment, while the segment containing the major arc is the major segment.
The centre of the circle lies in the major segment.
SECTOR OF A CIRCLE:
The region enclosed by an arc of a circle and its two bounding radii is called a sector of the circle.
In the given figure, OPRQO is a sector of the circle with centre O.
If arc PQ is a minor arc then OPRQO is called the minor sector of the circle.
The remaining part of the circle is called the major sector of the circle.
QUADRANT:
One-fourth of a circular disc is called a quadrant. The central angle of a quadrant is 90º.
FORMULAE:
Circumference and area of a circle
For a circle of radius r, we have
(i) Circumference of the circle = 2πr
(ii) Area of the circle = πr 2
(iii) Area of the semicircle = 1/2πr 2
(iv) Perimeter of the semicircle = (πr + 2r)
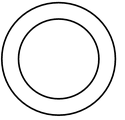
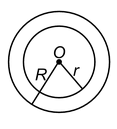
Area of a ring
Let R and r be the outer and inner radii of a ring.
Then, area of the ring = π(R 2 - r 2 ).
Rotating wheels
(i) Distance moved by a wheel in 1 rotation = circumference of the wheel
(ii) Number of rotations in 1 minute =

Rotation of the hands of a clock
(i) Angle described by the minute hand of a clock in 60 minutes = 360º.
(ii) Angle described by the hour hand of a clock in 12 hours = 360º.
Also Check
|
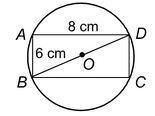
Question 1 . In figure, what is the ratio of the areas of a circle and a rectangle whose diameter and diagonal of a rectangle are respectively equal. |
|
Solution: Diagonal of a rectangle = BD = √6 2 + 8 2 = 10 cm.
It is given that : diagonal of rectangle = diameter of a circle
⇒ 10 = 2r ⇒r = 5.
∴

Question 2. What is the ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal?
Solution:
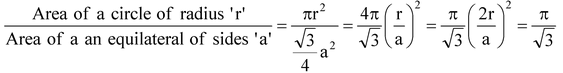 [a = 2r]
[a = 2r]
Question 3. The cost of fencing a circular field at the rate of Rs. 24 per metre is Rs. 5280. The field is to be ploughed at the rate of Rs. 0.50 per m2. Find the cost of ploughing the field (Take π = 22/7).
Solution: Length of the fence
= Total Cost/Rate = 5280/24 = 220m.
So, circumference of the field
= 220 m.
Therefore, if r metres is the radius of the field,
⇒ 2πr = 220 where r is the radius of field.
or
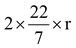 = 220
= 220
or r =
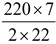 = 35 m
= 35 m
Therefore, area of the field
=
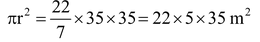
⇒ cost of ploughing 1m 2 of the field = Rs. 0.50.
So, total cost of ploughing the field
= Rs. 22 × 5 × 35 × 0.50 = Rs. 1925.
Question 4. A circular park, 42 m in diameter, has a path 3.5 m wide running round it on the outside. Find the cost of gravelling the path at Rs. 4 per m2.
|
Sol. Radius r of the circular park = 21 m. Radius R of the outer circle = (21 + 3.5) m = 24.5 m |
|
Area of the path = π[R 2 - r 2 ]
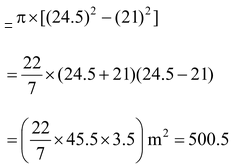
∴ Cost of gravelling the path = Rs. (500.5 ×4) = Rs. 2002.
Question 5. The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
Solution: The area of the circle having radius 8 cm
= π × (8) 2 ( r = 8 cm)
= 64 π cm 2 .
The area of the circle having radius 6 cm
= π × (6) 2
= 36 π cm 2.
Sum of the areas of the two circles
= (64 π + 36 π) cm 2 = 100 π cm 2 .
Let, if r be the radius of the circle which has area equal to the sum of the areas of the two given circles, then
πr 2 = 100 π
⇒ r 2 = 100
⇒ r = 10
Hence, the required radius is 10 cm.
Question 6. A bicycle wheel makes 5000 revolutions in moving 11 km. Find the diameter of the wheel.
Solution: Distance covered by the wheel in 1 revolution
=
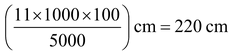
∴ The circumference of the wheel = 220 cm.
Let the diameter of the wheel be d cm.
Then, πd = 220
⇒
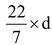 = 220
= 220
⇒ d =
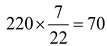
Hence, the diameter of the wheel is 70 cm.
Question 7. The diameter of the wheels of a bus is 140 cm. How many revolutions per minute must a wheel make in order to move at a speed of 66 km per hour?
Solution: Distance covered by a wheel in 1 minute
⇒
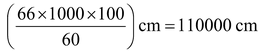
Circumference of a wheel
⇒ =
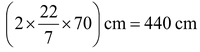
Number of revolutions in 1 min
⇒ (110000/440) = 250.
Question 8. A steel wire, when bent in the form of a square, encloses an area of 121 sq cm. The same wire is bent in the form of a circle. Find the area of the circle.
Solution: Side of the square = √121 cm = 11 cm
Perimeter of the square = (4 × 11) cm = 44 cm
∴ Length of the wire = 44 cm
∴ Circumference of the circle = Length of the wire = 44 cm
Let the radius of the circle be r cm
Then, 2πr = 44
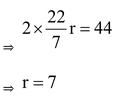
∴ Area of the circle = π r 2
=
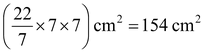 .
.
Do solve NCERT text book for class 10 maths with the help of Physics Wallah NCERT solutions for class 10 maths .