Areas Of Combinations Of Plane Figures
Area Related To Circles of Class 10
In the previous section, we have learnt to find areas of sectors and segments of a circle. In this section, we will learn to calculate the areas of some plane figures which are combinations of more than one plane figure.
|
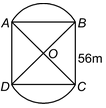
question 1. In the figure, two circular flowerbeds have been shown on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flowerbed is the point of intersection O of the diagonals of the square lawn, find the sum of the areas of the lawn and the flowerbeds. |
|
Solution: Area of the square lawn ABCD = (side)2 = 56 × 56 m2 ... (i)
Let OA = OB = x metres
In ΔAOB, ∠AOB = 90° [Diagonals of square bisect at 90°]
So, 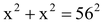 [By Pythagoras theorem]
[By Pythagoras theorem]
or, 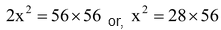 .. (ii)
.. (ii)
Now, area of sector OAB = 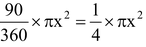
=  [From (ii)] ... (iii)
[From (ii)] ... (iii)
Also, area of ΔOAB = 
1/2 x 28 x 56 [∠AOB = 90º] ... (iv)
So area of flower bed AB = area of sector OAB − area of ΔOAB
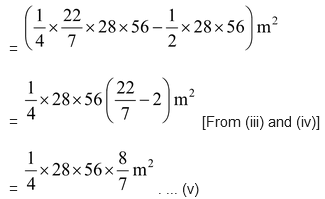
Similarly, area of the other flower bed
= 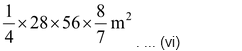 . ... (vi)
. ... (vi)
Therefore, total area
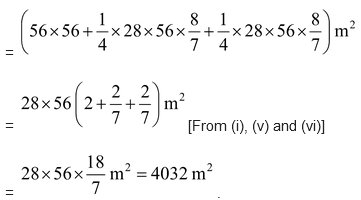
|
question 2. The inside perimeter of a running track, (figure) is 340 m. The length of each straight portion is 60 m, and the curved portions are semicircles. If the track is 7 m wide, find the area of the track. Also, find the outer perimeter of the track. |
|
Solution: Length of inner curved portion = (340 – 2 × 60) m = 220 m.
∴ The length of each inner curved part = 110 m.
Let the radius of each inner curved part be r.
Then πr = 110 m
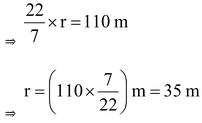
∴ Inner radius = 35 m, outer radius = (35 + 7) m = 42 m.
∴ Area of the track = (area of 2 rectangles) + (area of the circular ring)
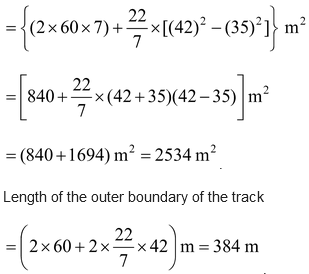
Hence, the outer perimeter of the track is 384 m.
|
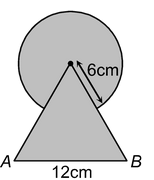
3. Find the area of the shaded region in the figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre. |
|
Solution: Area of the shaded region =
Area of the major sector of the circle + Area of the equilateral triangle OAB.
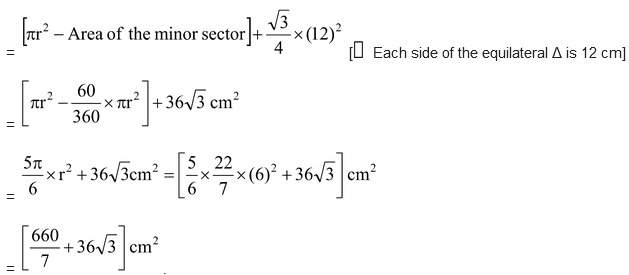
|
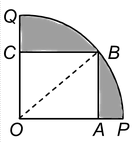
question 4. In the figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (π = 3.14). |
|
Solution: 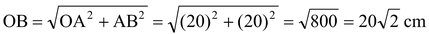 .
.
Then for the quadrant OPBQ, r = 20√2 cm.
The area of the shaded region
= The area of the quadrant OPBQ – The area of the square OABC
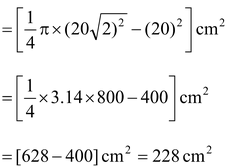
|
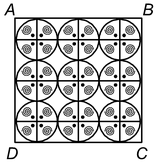
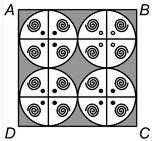
question 5. On a square handkerchief, nine circular designs each of radius 7 cm are made (figure). Find the area of the remaining portion of the handkerchief. Solution: Radius of the circle = 7 cm then diameter of the circle = 14 cm. then length of the side of the square ABCD = 3 × 14 cm = 42 cm. |
|
So, the total area of the handkerchief = (42)cm2 = 1764 cm2.
Area of the nine circular designs = 9 x πr2
= 9 x 22/7 (7)2 cm2 = 9 x 22 x 7 cm2 = 1386cm2.
Then the required area of the remaining portion
= 1764cm2 - 1386cm2 = 378cm2
|
question 6. Find the area of the shaded region in the figure, where ABCD is a square of side 14 cm. Solution: Area of square ABCD = 14 × 14 cm2 = 196 cm2. Diameter of each circle = 14/2 = 7cm. So, radius of each circle = 7/2 cm. |
|
So, area of one circle = πr2 = 22/7 x 7/2 x 7/2 cm2
= 77/2 cm2.
Therefore, area of the four circles = 4 x 77/2 cm2 = 154cm2.
Hence, area of the shaded region = (196 – 154) cm2 = 42 cm2.