Area Of Sector And Segment Of A Circle

Length of arc, area of sector and segment

Let an arc AB make an angle θ º < 180º at the centre of a circle of radius

Length of the arc =2πrθ/360

Perimeter of the sector OPRQO = OP + OQ + length of arc

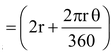
Area of the minor segment PRQP = (area of the sector OPRQO ΔOPQ)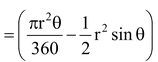

Area of the major segment QSPQ = (area of the circle) – (area of the minor segment PRQP)

Q: If the following figure is a sector of circle of radius 10.5 cm. Find the perimeter of the sector.

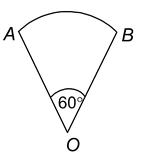
Sol. The arc length r = AB of a sector of an angle 60°in a circle of radius 10.5 cm is given by


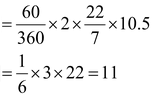
Perimeter of sector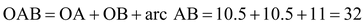

Q: In the following figure, the length of an arc AB = 20πcm is a sector of a circle, find the radius of the circle.

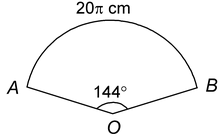
Sol.The arc of length AB= 20πcm of a sector of an angle 144° in a circle of radius ris given by

⇒cm.
Q: What is the ratio of the area of sector of angle 30 in a circle and that of the complete circle?
Sol.Area of a sector of angle 30°in a circle of radius r cm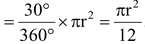

∴

Thus the ratio is 1 : 12.

Q: An arc of a circle is of length 5 cm and the sector is bounds has an area 20 π cm² . Find the radius of the circle.

Sol. We know that Area of a sector bounded by a given arc = 1/2 x (length of a given arc) radius of a circle.

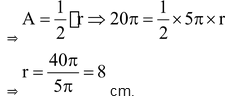
Q: The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.

Sol.Angle described by the minute hand in 60 minutes = 360º.
Angle described by the minute hand in 35 minutes 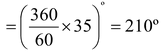  ⇒θ= 210º and r = 12 cm.

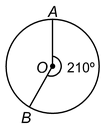
⇒Area swept by the minute hand in 35 minutes

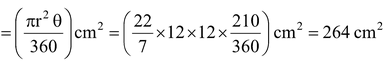
Q: The perimeter of a sector of a circle of radius 5.6 cm is 27.2 cm. Find the area of the sector.

Sol.Let O be the centre of a circle of radius 5.6 cm, and let OABO be its sector with perimeter 27.2 cm.
Then, OA + OB + arc AB = 27.2 cm.
⇒ 5.6 cm + 5.6 cm + arc AB = 27.2 cm.
⇒ arc AB= 16 cm.
Area of the sector OACBO

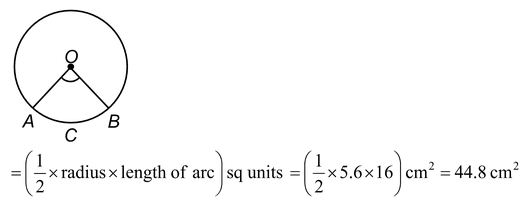
Q: An umbrella has 8 ribs, which are equally spaced (figure). Assume umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.

Sol.Here, r = 45º cm.
θ= sector angle between two consecutive ribs

360°/8= [ There are 8 sectors of same size] = 45º.
Therefore, the area between two consecutive ribs of the umbrella.
= The area of one sector.