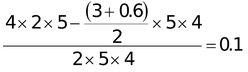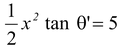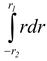Buoyancy: Archimedes’ Principle
Solids And Fluids of Class 11
Buoyancy: Archimedes’ Principle
If a body is partially or wholly immersed in a fluid, it experiences an upward force due to the fluid surrounding it.
The phenomenon of force exerted by fluid on the body called buoyancy and the force is called buoyant force.
A body experiences buoyant force whether it floats or sinks, under its own weight or due to other forces applied on it.
Archimedes Principle
A body immersed in a fluid experiences an upward buoyant force equivalent to the weight of the fluid displaced by it.
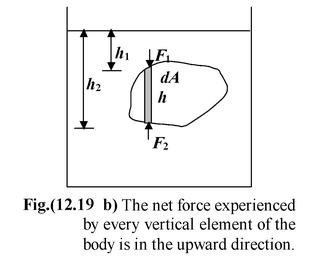
The proof of this principle is very simple. Imagine a body of arbitrary shape completely immersed in a liquid of density ρ as shown in the figure(12.19). A body is being acted upon by the forces from all directions. Let us consider a vertical element of height h and cross-sectional area dA as shown in the figure (12.19 b).
The force acting on the upper surface of the element is F1 (downward) and that on the lower surface is F2 (upward). Since F2> F1, therefore, the net upward force acting on the element is
dF = F 2 - F 1
It can be easily seen from the figure (12.19 b), that
F1 = (ρgh 1 )dA and F 2 = (ρgh 2 )dA
sodF = ρg(h)dA
Also,h 2 – h 1 = h andh(dA) = dV
∴The net upward force is
F =
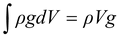
Hence, for the entire body, the buoyant force is the weight of the volume of the fluid displaced.
The buoyant force acts through the centroid of the displaced fluid.
|
|
|
IMPORTANT
The buoyant force arises because the pressure in the fluid is not uniform; it increases with depth.
An object floats on water if it can displace a volume of water whose weight is greater than that of the object. If the density of the material is less than that of the liquid, it will float even if the material is a uniform solid, such as a block of wood floats on water surface.
If the density of the material is greater than that of water, such as iron, the object can be made to float provided it is not a uniform solid. An iron hulled ship is an example to this case.
|
Example: 12.14
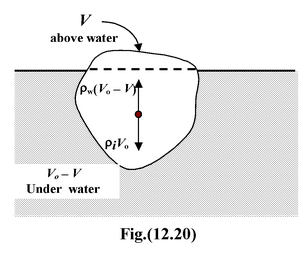
An iceberg with a density of
|
|
Solution
Let V be the volume of the iceberg above the water surface, then the volume under water will be Vo – V.
Under floating conditions, the weight (ρi Vog) of the iceberg is balanced by the buoyant force ρw(Vo – V))g. Thus,
ρiV o g = ρw(V o - V)g
orρwV = (ρw - ρi)V o
orρwV = (ρw - ρi)V o
or
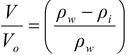
Sinceρw = 1025 kg m-3 and ρi = 920 kg m-3, therefore,
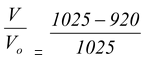 = 0.10
= 0.10
Hence 10 % of the total volume is visible.
Example: 12.15
When a 2.5 kg crown is immersed in water, it has an apparent weight of 22 N. What is the density of the crown?
Solution
Let W = actual weight of the crown
W′ = apparent weight of the crown
ρ = density of crown
ρ o = density of water
The buoyant force is given by
FB = W - W′
or ρ o Vg = W - W′
Since W = ρVg, therefore, V = W/ρg
Eliminating V from the above two equations, we get
ρ =
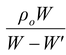
HereW = 25 N; W′ = 22 N; ρ o = 10 3 kg m -3
∴ρ = (10 3 )(25)/25-22 = 8.3 × 103 kg m-3
Stability of a Floating Body
The stability of a floating body depends on the effective point of application of the buoyant force. The weight of the body acts at its centre of gravity. The buoyant force acts at the centre of gravity of the displaced liquid. This is called the centre of buoyancy. Under equilibrium condition the centre of gravity G and the centre of buoyancy B lies along the vertical axis of the body as shown in the Fig. (12.21 a).
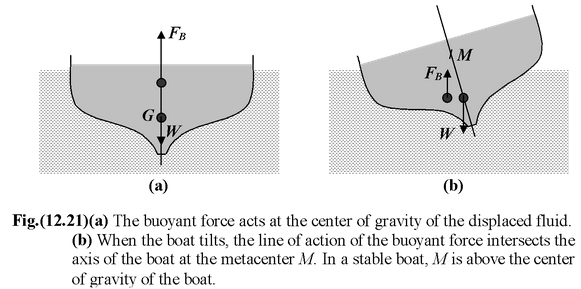
When the body tilts to one side, the centre of buoyancy shifts relative to the centre of gravity as shown in the figure (12.21 b). The two forces act along different vertical lines. As a result the buoyant force exerts a torque about the centre of gravity. The line of action of the buoyant force crosses the axis of the body at the point M, called the metacentre.
If G is below M, the torque will tend to restore the body to its equilibrium position.
If G is above M, the torque will tend to rotate the body away from its equilibrium position and the body will be unstable.
Example: 12.16
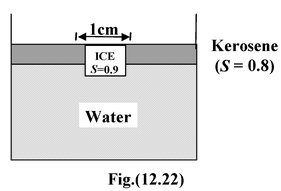
|
An ice cube of side 1cm is floating at the interface of kerosene and water in a beaker of base area 10 cm2. The level of kerosene is just covering the top surface of the ice cube. (a)Find the depth of submergence in the kerosene and that in the water. (b)Find the change in the total level of the liquid when the whole ice melts into water. |
|
Solution
(a)Condition of floating
0.8 ρwghk + ρwghw = 0.9 ρwgh
or0.8hk + hw = (0.9) h(1)
where hk and hw be the submerged depth of the ice in the kerosene and water, respectively.
Also,hk + hw = h(2)
Solving equations (1) and (2) , we get
hk = 0.5 cm , hw = 0.5 cm
(b)
Fall in the level of kerosene Δhk = 0.5/A
Rise in the level of water Δhw = 0.9 - 0.5 /A = 0.4/A
Net fall in the overall level
Δh = 0.1/A = 0.1/10 = 0.01 cm = 0.1 mm
|
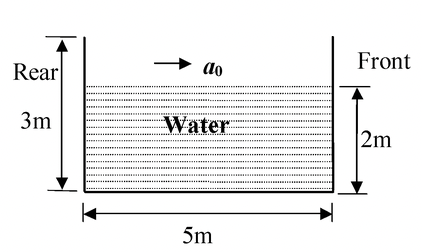
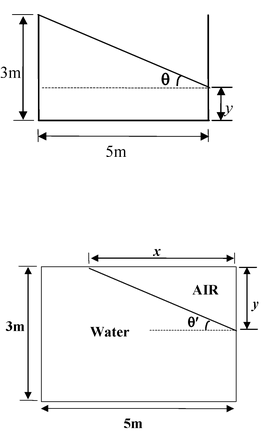
Example: 12.17 An open rectangular tank 5 m × 4 m × 3 m high containing water upto a height of 2 m is accelerated horizontally along the longer side. (a)Determine the maximum acceleration that can be given without spilling the water. |
|
(b) Calculate the percentage of water spilt over, if this acceleration is increased by 20%
(c) If initially, the tank is closed at the top and is accelerated horizontally by 9 m/s2, find the gauge pressure at the bottom of the front and rear walls of the tank. (Take g = 10 m/s2)
Solution
|
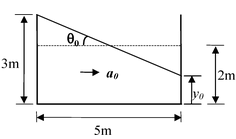
(a) Volume of water inside the tank remains constant (3 + y o /2) 5 x 4 = 5 x 2 × 4 or y 0 = 1m ∴ tan θ = 1 |
|
Since, tan θ 0 = a 0/g , therefore a0 = 0.4 g = 4 m/s2
|
(b) When acceleration is increased by 20% a = 1.2 a 0 = 0.48 g ∴ tan θ = a/g = 0.48 Now, y = 3-5 tan θ = 3 - 5(0.48) = 0.6 m Fraction of water spilt over
=
Percentage of water spilt over = 10% (c)a′ = 0.9g tan θ′ = a'/g = 0.9 volume of air remains constant 4 × 1/2 yx = (5) (1) × 4 Since y = x tan θ′
∴
or x = 3.33 m ; y = 3.0 m |
|
Gauge presure at the bottom of the
i) Front wall pf = zero
ii) Rear wall pr = (5tan θ′) ρwg = 5(0.9)(10 3 )(10) = 4.5 × 104 Pa
|
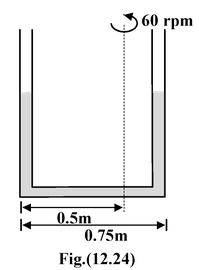
Example: 12.18 A vertical U - tube with the two limbs 0.75m apart is filled with water and rotated about a vertical axis 0.5m from the left limb , as shown in the figure(12.24). Determine the difference in elevation of the water levels in the two limbs. When the speed of rotation is 60 rpm. |
|
Solution
|
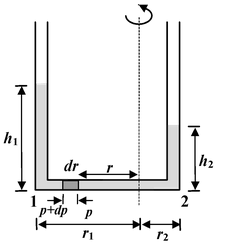
Consider a small element of length dr at a distance r from the axis of rotation. Considering the equilibrium of this element. (p + dp) - p = ρω 2 r dr ordp = ρω 2 r dr On integrating between 1 and 2 ,
p
1
- p
2
= ρω
2
|
|
p
1
- p
2
=
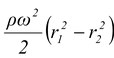
or h
1
- h
2
=
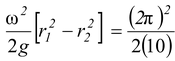 [(0.5)
2
- (0.25)
2
] = 0.37 m.
[(0.5)
2
- (0.25)
2
] = 0.37 m.
Also Check