Forces on Fluid Boundaries
Solids And Fluids of Class 11
Forces on Fluid Boundaries
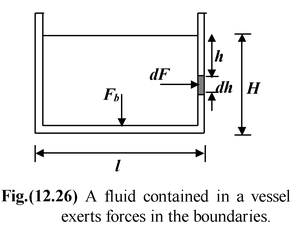
Whenever a fluid comes in contact with solid boundaries it exerts a force on it. Consider a rectangular vessel of base size l × b filled with water to a height H as shown in the fig.(12.26). The force acting at the base of the container is given by
|
Fb = p × (area of the base) because pressure is same everywhere at the base and is equal to ρgH. Therefore, Fb = ρgH(lb) = ρglbH Since lbH = V (volume of the liquid) Thus,Fb = ρgV = weight of the liquid inside the vessel |
|
Unlike the base, the pressure on the vertical wall of the vessel is not uniform but increases linearly with depth from the free surface. Therefore, we have to perform the integration to calculate the total force on the wall. Consider a small rectangular element of width b and thickness dh at a depth h from the free surface. The liquid pressure at this position is given by
p = ρgh
The force at the element is
dF = p(b dh) = ρgbh dh
The total force is F = ρgb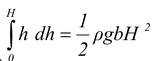
The total force acting per unit width of the vertical wall is
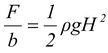 (12.23)
(12.23)
The point of application (the centre of force) of the total force from the free surface is given by
hc = 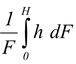 (12.24)
(12.24)
where 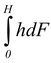 is the moment of force about the free surface.
is the moment of force about the free surface.
Here
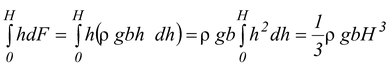
Since F = 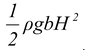 , therefore,
, therefore,
hc = 2/3H (12.25)
The net resultant force acts at a depth 2/3 H from the free surface.
Example: 12.19
|
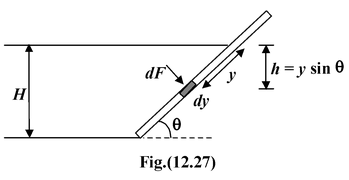
Find the force acting per unit width on a plane wall inclined at an angle θ with the horizontal as shown in the figure(12.27). |
|
Solution
Consider a small element of thickness dy at a distance y measured along the wall from the free surface. The pressure at the position of the element is
p = ρgh = ρgysinθ
The force is given by
dF = p(b dy) = ρgb(y dy) sin θ
The total force per unit width b is given by

Note that the above formula reduces to 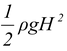 for a vertical wall (θ = 90o)
for a vertical wall (θ = 90o)
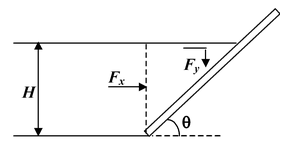
Alternatively, the force on the inclined wall may be obtained in two parts viz. horizontal and vertical.
|
The horizontal force Fx acts on the vertical projection of the incline wall, i.e. Fx = 1/2 ρgbH2 The vertical force Fy acts due to weight of the liquid supported by the wall, i.e. |
|
Fy = 1/2 ρgb(H)(H cot θ) = 1/2 ρgbH2 cotθ
The magnitude of the resultant force is given by
F = 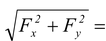 1/2 ρgbH2 cosec θ (12.27)
1/2 ρgbH2 cosec θ (12.27)
or F = 
- Introduction
- The States of Matter
- Stress, Strain and Elastic Modulii
- Stress – Strain Graphs
- Density and Pressure
- Fluid Statics
- Pressure Measuring Devices
- Buoyancy: Archimedes’ Principle
- Fluid Subjected to Constant Acceleration
- Forces on Fluid Boundaries
- The Equation of Continuity
- Bernoulli’s Equation
- Surface Tension
- Viscosity
- solved question
- Exercise 1