Bernoulli’s Equation
Solids And Fluids of Class 11
Bernoulli’s Equation
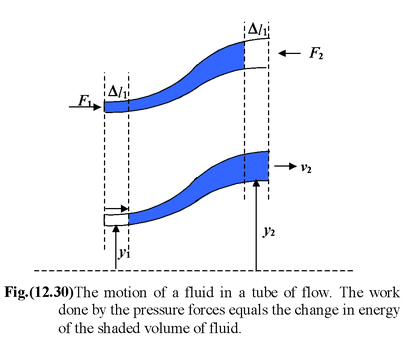
Bernoulli’s EquationLet us for our attention on the motion of the shaded region. This is our “system”. the lower cylindrical element of fluid of length Δl1 and area A1 is at height y1, and moves at cylindrical element of fluid of length Δl1 and area A1 is at height y1, and moves speed v1. After some time, the leading section of our system fills the upper cylinder of fluid of length Δl2 and area A2 at height y2, and is then moving speed v2. |
|
A pressure force F1 acts on the lower cylinder due to fluid to its left , and a pressure for F1 acts on the upper cylinder in the opposite direction. The net work done on the system by F1 and F2 is
W = F1Δl1 – F2Δl2 = P1A1Δl1 – P2A2Δl2 = (P1- P2)ΔV
where we have used the relations F = PA and ΔV = A1Δl1 = A2Δl2. The net effect of the motion of the system is to raise the height of the lower cylinder of mass Δm and to change its speed. The changes in the potential and kinetic energies are
ΔU = Δm g(y2 – y1)
ΔK = 1/2 Δm (v22 – v12)
These changes are brought about by the net work done on the system,
W = ΔU + ΔK
(P1 – P2)ΔV = Δmg(y2 – y1) + 1/2 Δm (v22 – v12)
Since the density is ρ = Δm/ΔV, we have
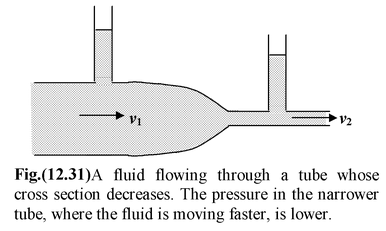
p1 + ρgy1 + 1/2 ρv12 = p2 + ρgy2 + 1/2 ρv22
Since the points 1 and 2 can be chosen arbitrarily, we can express this result as Bernoulli’s Equation
p + ρgy + 1/2ρv2 = constant (12.30)
|
Daniel Bernoulli derived this equation in 1738. It is applied to all points along a streamline in a nonviscous, incompressible fluid. |
|
Example: 12.20
|
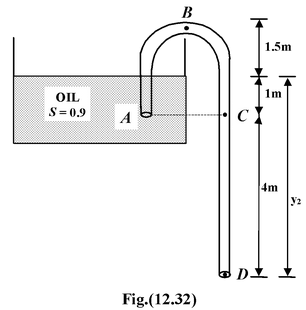
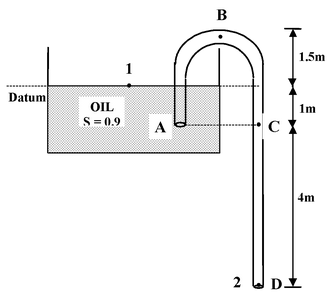
A siphon tube is discharging a liquid of specific gravity 0.9 from a reservoir as shown in the figure(12.32). (a) Find the velocity of the liquid through the siphon (b) Find the pressure at the highest point B. (c) Find the pressure at the points A(out side the tube) and C. State and explain the following : (d) Would the rate of flow be more, less or the same if the liquid were water ? (e) Is there a limit on the maximum height of B above the liquid level in the reservoir. (f) Is there a limit on the vertical depth of the right limb of the siphon. |
|
Solution
Assume datum at the free surface of the liquid.
(a) Applying Bernoulli’s equation on point 1 and 2 , as shown in the figure.

Here p1 = p2 = p0 = 105 N/m2 ; y1 = 0, y2 = -5 m
Since area of the tube is very small as compared to that of the reservoir, therefore,
v1 << v2 . thus 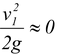
|
Here, p1 = 105 N/m2 ; y1 = 0, vB = v2 = 10 m/s, yB = 1.5 m
∴pB = p1 - |
|
or pB = 105 - 1/2 (900)(10)2 - (900)(10)(1.5) = 41.5 kN/m2
(c) Applying Bernoulli’s equation at 1 and A
pA = p1 + ρg (y1 - yA)
orpA = 105 + (900)(10)(1) = 109 kN/m2.
Applying Bernoulli’s equation at 1 and C,
pC = p1 - 1/2 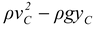
= 105 - 1/2 (900)(10)2 - (900)(10)(-1) = 105 - 45000 + 9000 = 64 kN/m2.
(d) The velocity of flow is independent of the density of the liquid , therefore, the discharge would remain the same.
(e) Since the pressure at B is less than atmospheric, the liquid, therefore, has a tendency to get vapourised if the pressure becomes equal to the vapour pressure of it. Thus , pB > pvapour.
(f) The velocity of flow depends on the depth of the point D, below the free surface
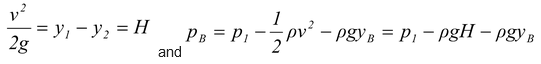
For working of siphon , H ≠ 0, and H should not be high enough so that pB may not reduce to vapour pressure.
Example: 12.21
A garden hose has an inside cross-sectional area of 3.60 cm2, and the opening in the nozzle is 0.250 cm2. If the water velocity is 50 cm/s in a segment of the hose that lies on the ground
(a) with what velocity does the water come from the nozzle when it is held 1.50 m above the ground and
(b) What is the water pressure in the hose on the ground?
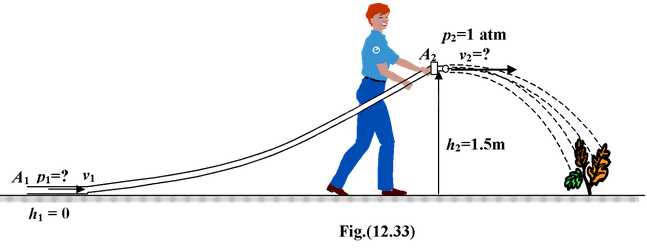
Solution
(a) The problem is illustrated in figure. We first apply the Equation of Continuity. Equation (), to find the velocity of the fluid at the nozzle.
v2 = 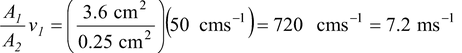
(b) We next apply Bernoulli’s Equation to find the pressure p1. We know that
h1 = 0 and h1 = 1.5 m.
The pressure at the nozzle is atmospheric pressure
p2 = 1.01 × 105 Pa.
Solving for p1 and using the density of water
ρ = 1 × 103 kg/m3, we have
p1 = p2 + 1/2 ρ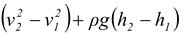
= (1.01 × 105) + 1/2(1 × 103)[(7.2)2 – (0.50)2]
+ (1 × 103)(9.8)(1.5 – 0) = 1.41 × 105 Pa
Example: 12.22
|
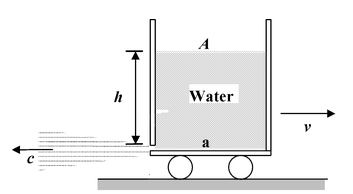
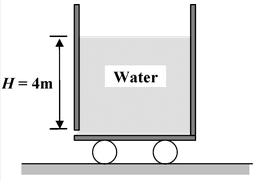
A tank, intially at rest, is filled with water to a height H = 4 m. A small orifice is made at the bottom of the wall. Find the velocity attained by the tank when it becomes completely empty. Assume mass of the tank to be negligible. Friction is negligible. Solution |
|
Let v be the instantaneous velocity of the tank, and c be the instantaneous velocity of efflux with respect to the tank.
Thrust exerted on the tank is
F = ρac2
where a is the cross-sectional area of the orifice.
c = √2gh
where h is the instantaneous height of water in the tank.
|
Mass of the tank at any time t is m = ρAh A = cross-sectional area of the tank. Using Newton’s second law
|
|
or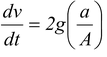 (1)
(1)
In a time dt if the water level falls by dh, then according to the conservation of mass.

Equation (1) can be written as

On integrating
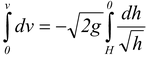
v = 2√2gH
Since H = 4 m,
therefore v = 2√2(10)(4) = 17.9 m/s
- Introduction
- The States of Matter
- Stress, Strain and Elastic Modulii
- Stress – Strain Graphs
- Density and Pressure
- Fluid Statics
- Pressure Measuring Devices
- Buoyancy: Archimedes’ Principle
- Fluid Subjected to Constant Acceleration
- Forces on Fluid Boundaries
- The Equation of Continuity
- Bernoulli’s Equation
- Surface Tension
- Viscosity
- solved question
- Exercise 1
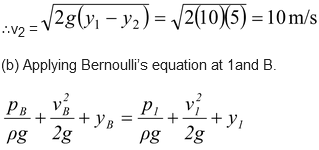
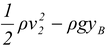
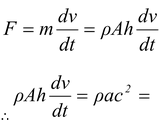 2ρgah
2ρgah