Important Questions for Class 10 Maths Chapter 11:
In Chapter 11 of Class 10 Mathematics, "Constructions," students are introduced to fundamental geometric constructions involving line segments, similar triangles, and tangents to circles. These constructions form the basis of various mathematical concepts and are essential for problem-solving in geometry.
To facilitate effective exam preparation for the Class 10 board exams 2023-2024, a set of important questions for Construction has been compiled based on the latest CBSE pattern. By practicing these important questions, students can enhance their construction skills, familiarize themselves with the types of questions likely to appear in the exam, and to score good marks. Moreover, referring to these questions alongside NCERT Solutions available at Physics Wallah provides comprehensive support for students in mastering the concepts in the Class 10 Maths paper.
Important Questions for Class 10 Maths Chapter 11 Overview
The Important Questions for Class 10 Maths Chapter 11 have been provided by Physics Wallah in a format that is easy for students to understand and study. These questions closely resemble those that students may encounter in the actual board exam paper. By practicing these questions, students can gain a better understanding of the chapter's concepts and improve their problem-solving skills.
Physics Wallah emphasis on providing questions in an accessible format ensures that students can effectively prepare for the Class 10 Maths exam and feel confident when facing similar questions in the actual paper.
Important Questions for Class 10 Maths Chapter 11
Q.1:
Draw a triangle ABC in which AB = 5 cm, BC = 6 cm and ∠ABC = 60°. Then construct a triangle whose sides are
5
7
times the corresponding sides of ∆ABC. (2011D)
Solution:
In ∆ABC
AB = 5 cm
BC = 6 cm
∠ABC = 60°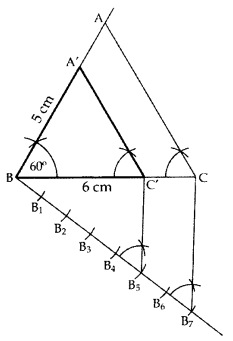
Hence, ∆A’BC’ is the required ∆.
Q.2: Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameters, each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Solution:
Steps of construction:
Step 1: Draw a circle with a radius of 3 cm with centre “O”.
Step 2: Draw a diameter of a circle with endpoints P and Q, and it extends 7 cm from the centre.
Step 3: Draw the perpendicular bisector of the line PO and mark the midpoint as M.
Step 4: Draw a circle with M as centre and MO as the radius
Step 5: Now join the points PA and PB in which the circle with radius MO intersects the circle at points A and B.
Step 6: Now PA and PB are the required tangents.
Step 7: Similarly, from point Q, we can draw the tangents.
Step 8: From that, QC and QD are the required tangents.
Q.3:
Construct a right triangle in which the sides, (other than the hypotenuse) are of length 6 cm and 8 cm. Then construct another triangle, whose sides are
3
5
times the corresponding sides of the given triangle.
Solution:
Here AB = 8 cm, BC = 6 cm and
Ratio =
3
5
of corresponding sides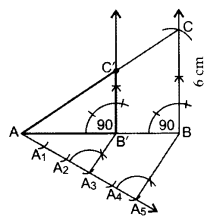
∴ ∆AB’C’ is the required triangle.
Q.4: Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on the outer circle, construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
Solution:
Steps of construction:
Step 1: Draw a circle with centre O and radius 3 cm.
Step 2: Draw another circle with centre O and radius 5 cm.
Step 3: Take a point P on the circumference of a larger circle and join OP.
Step 4: Draw another circle such that it intersects the smallest circle at A and B.
Step 5: Join A to P and B to P.
Q.5:
Draw a triangle ABC with BC = 7 cm, ∠B = 45° and ∠C = 60°. Then construct another triangle, whose sides are
3
5
times the corresponding sides of ∆ABC. (2012OD)
Solution:
Here, BC = 7 cm, ∠B = 45°, ∠C = 60° and ratio is
3
5
times of corresponding sides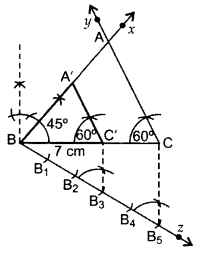
∴ ∆A’BC’ is the required triangle.
Q.6:
Draw a pair of tangents to a circle of radius 3 cm, which are inclined to each other at an angle of 60°. (2011OD)
Solution:
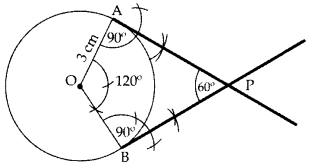∴ PA & PB are the required tangents.
Q.7: Construct an equilateral ΔABC with each side 5 cm. Then construct another triangle whose sides are 2/3 times the corresponding sides of ΔABC.
Solution:
Steps of construction:
Step 1:
Draw a line segment BC = 5 cm.
Step 2:
Taking B as centre and radius 5 cm, draw an arc.
Step 3:
Now, taking C as centre and radius 5 cm, draw another arc meeting the previous arc at point A.
Step 4:
Now join point AC and BC. Thus ΔABC is the required triangle.
Step 5:
Draw a line BX such that ∠CBX is an acute angle and is opposite of vertex A.
Step 6:
Along BX, mark 3 points B
1
, B
2
, B
3
such that BB
1
= B
1
B
2
= B
2
B
3
.
Step 7:
Now join B
3
to C.
Step 8:
Draw a line B
2
C’ || B
3
C
Step 9:
Draw a line A’C’ parallel to AC.
Q.8: Draw a pair of tangents to a circle of radius 4.5 cm, which are inclined to each other at an angle of 45°.
Solution:
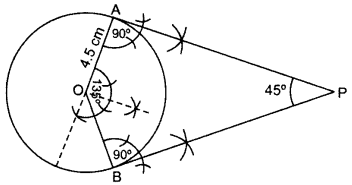Draw ∠AOB = 135°, ∠OAP = 90°, ∠OBP = 90°
∴ PA and PB are the required tangents.
Q:9. Draw two tangents to a circle of radius 3.5 cm, from a point P at a distance of 6.2 cm from its cehtre.
Solution:
OP = OC + CP = 3.5 + 2.7 = 6.2 cm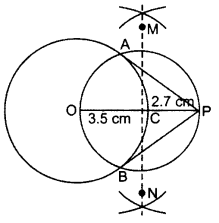
Hence AP & PB are the required tangents.
Q.10:
Construct a ΔABC in which AB = 6 cm, ∠A = 30° and ∠B = 60°. Construct another ΔAB’C’ similar to ΔABC with base AB’ = 8 cm.
Solution:
Given, AB = 6 cm and AB’ = 8 cm
Scale factor = AB’/AB = 8/6 = 4/3
Steps of construction:
Step 1: Draw a line segment AB = 6 cm.
Step 2: At A and B, construct angles 30° and 60° respectively and let these lines intersect each other at C. Thus ΔABC is the required triangle.
Step 3: Draw a line AX such that ∠BAX is an acute angle and is opposite of vertex C.
Step 4: Along AX, mark 4 points A1, A2, A3, A4 such that AA1 = A1A2 = A2A3 = A3A4
Step 5: Now join A3B.
Step 6: Draw a line through A4 which is parallel to A3B such that it intersects the extended AB at B’.
Step 7: Draw a line B’C’ parallel to BC such that it meets the extended AC at C’.
Q.11: Draw a triangle ABC with side BC = 7 cm, ∠B = 45° and ∆A = 105°. Then construct a triangle whose sides are
3
5
times the corresponding sides of ∆ABC. (2011D)
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180° … [angle sum property of a ∆
105° + 45° + C = 180°
∠C = 180° – 105° – 45o = 30°
BC = 7 cm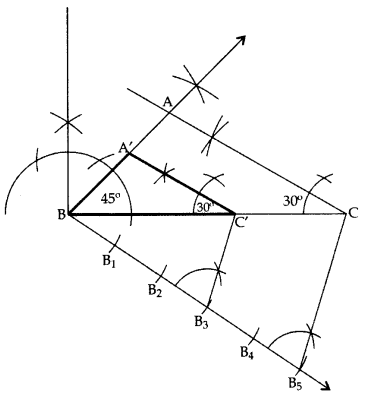
∴ ∆A’BC’ is the required ∆.
Q.12:
Draw a triangle ABC with side BC = 6 cm, ∠C = 30° and ∠A = 105°. Then construct another triangle whose sides are
2
3
times the corresponding sides of ∆ABC. (2012D)
Solution:
Here, BC = 6 cm, ∠A = 105o and ∠C = 30°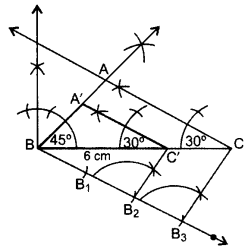
In ∆ABC,
∠A + ∠B + ∠C = 180° …[Angle-sum-property of a ∆
105° + ∠B + 30o = 180°
∠B = 180° – 105° – 30o = 45°
∴ ∆A’BC’ is the required ∆.
Q.13: Construct an isosceles triangle whose base is 6 cm and altitude 4 cm. Then construct another triangle whose sides are
3
4
times the corresponding sides of the isosceles triangle.
Solution:
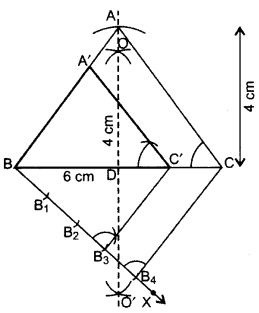∴ ∆A’BC’ is the required triangle.
Q. 14: Draw a line segment AB of length 7 cm. Taking A as centre, draw a circle of radius 3 cm and taking B as centre, draw another circle of radius 2 cm. Construct tangents to each circle from the centre of the other circle.
Solution:
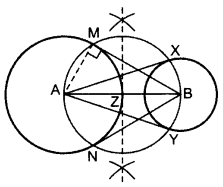Draw two circles on A and B as asked.
Z is the mid-point of AB.
From Z, draw a circle taking ZA = ZB as radius,
so that the circle intersects the bigger circle at M and N and smaller circle at X and Y.
Join AX and AY, BM and BN.
BM, BN are the required tangents from external point B.
AX, AY are the required tangents from external point A.
Justification:
∠AMB = 90° …[Angle in a semi-circle
Since, AM is a radius of the given circle.
∴BM is a tangent to the circle
Similarly, BN, AX and AY are also tangents.
Q.15: Draw an isosceles ∆ABC in which BC = 5.5 cm and altitude AL = 3 cm. Then construct another triangle whose sides are
3
4
of the corresponding sides of ∆ABC.
Solution:
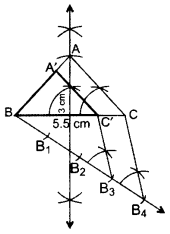∴ ∆ABC’ is the required ∆.
Benefits of Solving Important Questions for Class 10 Maths Chapter 11
Understanding Concepts:
By solving these questions, students deepen their understanding of geometric construction techniques, including drawing precise line segments, constructing similar triangles, and finding tangents to circles.
Exam Preparation:
These questions are designed to align with the CBSE exam pattern, giving students a clear idea of the types of questions that may appear in the board exams. By practicing these questions, students can familiarize themselves with the exam format and improve their performance.
Enhanced Problem-Solving Skills:
Geometric constructions require logical thinking and spatial reasoning, and practicing these questions helps students develop these skills. They learn to apply construction techniques effectively to solve a variety of problems.
Improved Confidence:
As students successfully solve these questions, their confidence in their ability to tackle construction-related problems increases. This confidence is essential for performing well in the Class 10 Maths exam.
Better Time Management:
Working through these questions helps students improve their time management skills. They learn to allocate time efficiently to different types of construction problems, ensuring they can complete the exam within the allotted time frame.
