RD Sharma Solutions Class 9 Maths Chapter 2:
This RD Sharma Solutions for Class 9 Maths Chapter 2 on Exponents of Real Numbers assist students in grasping concepts like integral exponents of a real number, laws of exponents, and rational powers.
These solutions are provided here for free, enabling easy learning and understanding of the concepts related to exponents of Real Numbers. Students can download the RD Sharma Solutions for Class 9 Maths Chapter 2 in PDF format. Practicing textbook questions using these solutions enhances conceptual knowledge among students. For those aiming to secure high marks, it is recommended to download the solutions in PDF format from the provided link.
CBSE Class 9 Science Syllabus 2024-25
Students can use the RD Sharma Solutions for Class 9, which has been solved by subject matter experts in compliance with the CBSE syllabus, if they want to score highly on exams. Students will study several crucial procedures for solving real numbers in Chapter 2.
RD Sharma Solutions Class 9 Maths Chapter 2 PDF
The PDF link for RD Sharma Class 9 Solutions for Maths Chapter 2 on Exponents of Real Numbers is provided below. This PDF contains detailed solutions to all the exercises in the chapter, helping students understand the concepts better and strengthen their problem-solving skills.
By referring to these solutions, students can enhance their preparation for exams and aim to achieve better grades in mathematics. Access the PDF link below to download the solutions and start practicing.
RD Sharma Class 9 Solutions Maths Chapter 2 PDF
RD Sharma Solutions Class 9 Maths Chapter 2 Exponents of Real Numbers
The solutions for RD Sharma Class 9 Maths Chapter 2 on Exponents of Real Numbers are provided below. These solutions provide step-by-step explanations to help students understand the concepts thoroughly.
CBSE Class 10 Result 2024 Expected To Be Out Soon
With comprehensive solutions available, students can strengthen their grasp of mathematical concepts and prepare effectively for exams. Access the solutions below to enhance your understanding of exponents and score good marks in mathematics.
RD Sharma Solutions Class 9 Maths Chapter 2 Exercise 2.1
Question 1: Simplify the following
(i) 3(a
4
b
3
)
10
x 5 (a
2
b
2
)
3
(ii) (2x
-2
y
3
)
3
Solution:
Using laws: (a
m
)
n
= a
mn
, a
0
= 1, a
-m
= 1/a and a
m
x a
n
= a
m+n
]
(i)
3(a
4
b
3
)
10
x 5 (a
2
b
2
)
3
On simplifying the given equation, we get;
= 3(a
40
b
30
) x 5 (a
6
b
6
)
= 15 (a
46
b
36
)
[using laws: (a
m
)
n
= a
mn
and a
m
x a
n
= a
m+n
]
(ii)
(2x
-2
y
3
)
3
On simplifying the given equation, we get;
= (2
3
x
-2 × 3
y
3×3
)
= 8 x
-6
y
9
(iii)
Question 2: If a = 3 and b =-2, find the values of:
(i) a
a
+ b
b
(ii) a
b
+ b
a
(iii) (a+b)
ab
Solution
:
(i)
a
a
+ b
b
Now putting the values of ‘a’ and ‘b’, we get;
= 3
3
+ (−2)
−2
= 3
3
+ (−1/2)
2
= 27 + 1/4
= 109/4
(ii)
a
b
+ b
a
Now putting the values of ‘a’ and ‘b’, we get;
= 3
−2
+ (−2)
3
= (1/3)
2
+ (−2)
3
= 1/9 – 8
= −71/9
(iii)
(a+b)
ab
Now putting the values of ‘a’ and ‘b’, we get;
= (3 + (−2))
3(−2)
= (3–2))
−6
= 1
−6
= 1
Question 3: Prove that
Solution
:
(i)
L.H.S. =
= R.H.S.
(ii)
We have to prove here;
L.H.S. =
=R.H.S.
(iii)
L.H.S. =
= R.H.S.
Question 4: Prove that
Solution
:
(i)
L.H.S
= R.H.S.
(ii)
L.H.S
= R.H.S.
Question 5: Prove that
Solution
:
(i)
L.H.S.
= R.H.S.
(ii)
L.H.S.
= R.H.S.
Question 6: If abc = 1, show that
Solution:
RD Sharma Solutions Class 9 Maths Chapter 2 Exercise 2.2
Question 1: Assuming that x, y, z are positive real numbers, simplify each of the following:
Solution:
Question 2: Simplify
Solution:
Question 3: Prove that
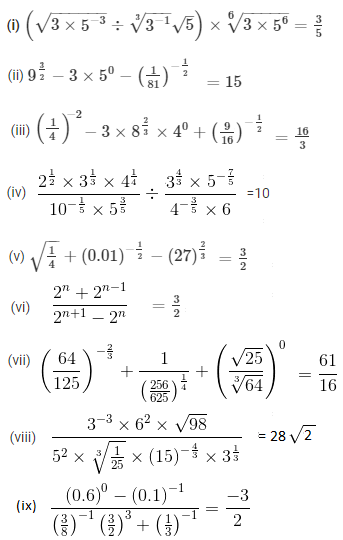
Solution:
(i) L.H.S.
=R.H.S.
Question 4.
Show that:
Solution
:
RD Sharma Solutions Class 9 Maths Chapter 2 Exercise-VSAQs
Question 1: Write (625)
–1/4
in decimal form.
Solution:
(625)
–1/4
= (5
4
)
-1/4
= 5
-1
= 1/5
= 0.2
Question 2: State the product law of exponents:
Solution
:
To multiply two parts having same base, add the exponents.
Mathematically:
x
m
x x
n
= x
m +n
Question 3: State the quotient law of exponents.
Solution:
To divide two exponents with the same base, subtract the powers.
Mathematically:
x
m
÷ x
n
= x
m – n
Question 4: State the power law of exponents.
Solution:
Power law of exponents :
(x
m
)
n
= x
m x n
= x
mn
Question 5: For any positive real number x, find the value of
Solution
:
Question 6: Write the value of {5(8
1/3
+ 27
1/3
)
3
}
1/4
.
Solution:
{5(8
1/3
+ 27
1/3
)
3
}
1/4
= {5(2
3×1/3
+ 3
3×1/3
)
3
}
1/4
= { 5(2 + 3)^3}
1/4
= (5
4
)
1/4
= 5
RD Sharma Solutions for Class 9 Maths Chapter 2 Exponents of Real Numbers Summary
In the 2nd chapter of RD Sharma Solutions for Class 9, students will delve into significant concepts regarding Exponents of Real Numbers, encompassing the following:
-
Introduction to Exponents of Real Numbers
-
Integral exponents of a Real Number
-
Laws of Integral Exponents
-
Rational Exponents of Real Number
-
nth root of a positive Real Number
-
Laws of Rational Exponents
