
NCERT Solutions For Class 11 Maths chapter-10 Straight Lines Miscellaneous Exercise
NCERT Solutions for Class 11 Maths Chapter-10 Straight LInes
Academic team of Physics Wallah developed step by step NCERT Solutions for Class 11 Maths Chapter-10 Straight LInes Miscellaneous Exercise according to recommen dations and Guideline of CBSE. You can download and share NCERT Solutions for Class 11 Maths.
Question 1. Find the values of k for which the line (k−3)x − (4−k 2 )y + k 2 −7k + 6=0
(a) Parallel to the x-axis,
(b) Parallel to the y-axis,
(c) Passing through the origin.
Solution :
Given:
Equation of line
(k−3)x − (4−k
2
)y + k
2
−7k + 6=0
If the line is parallel to
x-axis,
Slope of the line = Slope of the
x-axis
(a) If the line parallel to x-axis, then lope of the line = Slope of the x-axis
it can be writen as (k−3)x − (4−k 2 )y + k 2 −7k + 6=0
we get
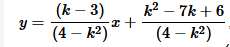
Which is of the form
y = mx + c
Here, the slope of the given line
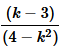
Consider the slope of x-axis =0
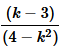 = 0
= 0
k−3=0
k=3
Therefore, if the given line is parallel to the x
-axis, then the value of k is 3
.
(b) If the line parallel to y-axis, then
The given equation of line is
(k−3)x − (4−k
2
)y + k
2
−7k + 6=0
Here if the line is parallel to the y-axis, it is vertical and the slope will be undefined.
So, the slope of the given line =
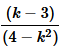
Here, (k−3) / (4−k
2
) is undefined at k2=4
k
2
= 4
⇒k=±2
Therefore, if the given line is parallel to the y
-axis, then the value of k is ±2.
(c) If the line passes through origin then
The given equation of line is (k−3)x − (4−k
2
)y + k
2
− 7k + 6 = 0
Here, if the line is passing through (0,0)
which is the origin satisfies the given equation
of line,
(k−3)(0) − (4−k
2
) (0)+k
2
−7k+6=0
k
2
−7k+6=0
Separate the terms,
k
2
−6k−k+6=0
(k−6)(k−1)=0
k=1or 6
Therefore, if the given line is passing through the origin, then the value of k
is either
1or 6
Question 2. Find the values of θ and p, if the equation x cos θ + y sinθ = p is the normal form of the line √3x + y + 2=0.
Solution :
Given:
√3x + y + 2=0.
3x + y = -2
Dividing both sides by
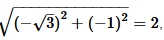 ,
,
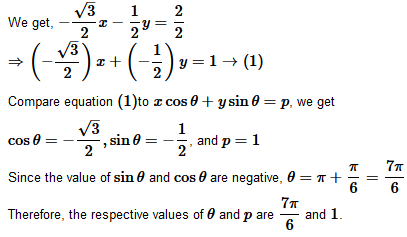
Question 3. Find the equations of the lines which cut-off intercepts on the axes whose sum and product are 1 and -6 respectively.
Solution
:Consider, the intercepts cut by the given lines on the axes are a
and b.
a + b = 1→(1)(1)
ab = − 6 → (2)
Solve both the equations to get
a = 3 and b = −2 or a = −2 and b = 3
We know that the equation of the line whose intercepts on a and b axes is
xa + yb = 1
or
bx + ay − ab = 0
Case 1:
a = 3
and b = −2
Now, the equation of the line is
−2x + 3y + 6 = 0
That is,
2x − 3y = 6
Case 2:
a=−2
and b=3
Now, the equation of the line is 3x − 2y + 6 = 0
That is, −3x + 2y = 6
Therefore, the required equation of the lines are 2x − 3y = 6
and −3x + 2y = 6.
Question 4. What are the points on the y-axis whose distance from the line x/3 + y/4 = 1 is 4 units?
Solution :
Given: Equation of line (0,b) and let point on
x/3 + y/4 = 1
axis be 4
it can be writen as 4x + 3y -12 = 0 → (1)
compare equation (1) to the perpendicular distance (d) of a line
4x + 3y -12 = 0
A = 4,B = 3 and C = −12
We know that the perpendicular distance (d) of a line Ax+By+C=0 from (x1,y1) is,

Question 5. Find perpendicular distance from the origin to the line joining the points (cosθ, sin θ) And (cosϕ,sinϕ).
Solution :
Equation of the line joining points
(cosθ, sin θ)
and
(cosϕ,sinϕ)
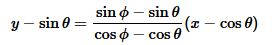
y(cosϕ − cosθ) − sinθ(cosϕ − cosθ)
=x(sinϕ − sinθ) − cosθ(sinϕ − sinθ)x (sinθ − sinϕ) − y(cosϕ − cosθ) + cosθ sinϕ − cosθsinθ − sinθ cosϕ + sinθ cosθ
=0x(sinθ − sinϕ) + y(cosϕ − cosθ) + sin(ϕ−θ)=0
Ax + By + C=0, where A
= sinθ − sinϕ,B= cosϕ − cosθ, and C=sin(ϕ−θ)
It is known that the perpendicular distance (d) of a line Ax + By + C = 0 from a point (x 1 , y 1 ) is given by d= |Ax 1 + By 1 + C| / √A 2 +√B 2 .
Therefore, the perpendicular distance (d) of the given line from point (x1, y1) = (0, 0) is

Question 6. Find the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x – 7y + 5 = 0 and 3x + y = 0.
Solution :
The equation of any line parallel to the y-axis is of the form x = a → (1)
The two given lines are x−7y + 5 = 0 → (2)
3x + y = 0 → (3)
Solve equation (2) and (3)
, we get x = −5 / 22 and y = 15 / 22
Thus, (−5 / 22 , 15 /22)
is the point of intersection of lines (2) and (3).
Since line x = a passes through point (−5 / 22,15 / 22),
a = −5 /22
Therefore, the required equation of the line is x = −5 22
Question 7. Find the equation of a line drawn perpendicular to the line x/4 + y/6 = 1 through the point, where it meets the y-axis.
Solution :
Given: Equation of line
x/4 + y/6 = 1
Here, the equation of the given line is x
/
4
+
y
/
6
=
1
This equation can be written as 3x + 2y − 12 = 0
Rewrite as,
y=−3 / 2x + 6
, which is of the form y = mx + c
Now, Slope of the given line = −3 / 2
∴Slope of line perpendicular to the given line = −1 / (−3/2 ) = 2 / 3
Let the given line intersect the y-axis at (0,y)
.
Substitute x with 0 in the equation of the given line,
y / 6 = 1
⇒ y = 6
∴ The given line intersects the y-axis at (0,6)
The equation of the line that has a slope of 23 and passes through point (0,6) is,(y−6)=23(x−0) Cross multiply and expand brackets,
3y − 18 = 2x
2x − 3y + 18 = 0
Therefore, the required equation of the line is 2x − 3y + 18 = 0
.









